Fundamentals of Radio Astronomy

Joachim Köppen Strasbourg 2010

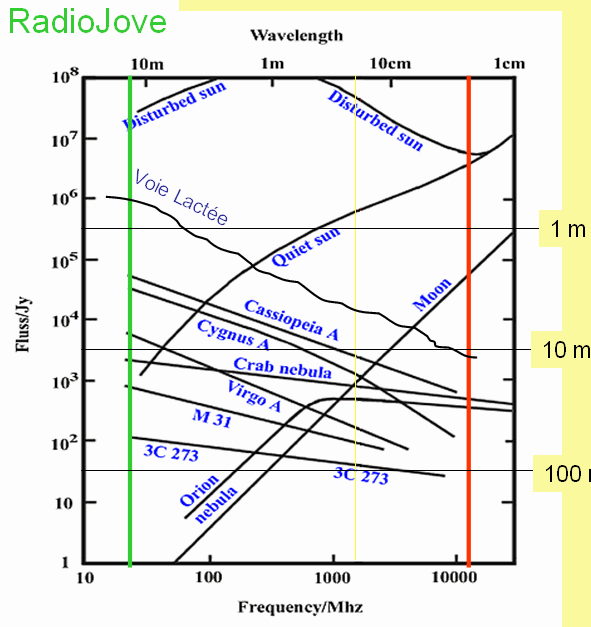
This is the radio spectrum of astronomical sources (from the book "Radioastronomy" by John Kraus, W8JK). The green line marks 20 MHz, the frequency on which our RadioJove telescope had worked until 2009 (and captured radio bursts from the Sun). The yellow line indicates the wavelength of 21cm, which is observed by the ESA-Haystack telescope. The red line marks 12 GHz, where the ESA-Dresden telescope works. The vertical axis is the flux of the sources, that is the power per unit surface area of the telescope. The horizontal lines marked with 1m, 10m, and 100m indicate the sensitivity that can be achieved by radio telescopes of that diameter: they show the fluxes which correspond to the thermal noise produced in the receiver itself (at room temperature).

Here is a JAVA applet which is an "animation" of the above plot. Clicking on the plot, you can read off the fluxes, apparent brightness temperatures (if one assumed a unity solid angle for the source), antenna temperatures and signal-to-noise ratios for a given antenna size.

Introductory material on radio astronomy

There is a wealth of material on various aspects of radio astronomy available on the Internet, either by professional institutions or by dedicated amateurs. It is well worth "googling" for a while on the Net to find information suited to one's particular taste and level. Here are a few references that we found quite useful:

• Book on RadioJove telescope by Richard Flagg: while primarily aimed for the observation on 20 MHz of Jupiter and the Sun, this well-written book contains several chapters which also serve well as an introduction to radio astronomy.
• MIT Haystack Radio Astronomy Tutorial gives a good introduction to the basic concepts.
• Radio Astronomy Course by Dale E.Gary is a graduate lecture course, which is a good introduction to the subject, with good plots and images. Some parts will be too advanced for our purposes. Also, there are a number of interesting links.
• Itty Bitty Radio Telescope is primarily about a very simple approach to 10 GHz radio astronomy, but it also contains some very valuable links for background information.

• SARA is the website of the Society of Amateur Radio Astronomers, and presents a lot of good material and projects.

Some essential definitions and relations

For the interpretation of observations it is necessary to clarify how we measure radiation. In particular, we have to distinguish between two quantities, the flux and the intensity. In radio astronomy, we speak of antenna temperature and brightness temperatures:

• the flux (or more accurately: the flux density) F (or often: S) is the power per unit frequency interval that passes through a surface of unit area. Thus the power density received by our antenna is P = F * A / 2 where A is the (effective) cross section of the antenna dish. There is a reduction by a factor 2, because we observe in horizontal or vertical polarization only.
• for the small fluxes encountered in radio astronomy it is convenient to define the unit 1 Jansky = 1 Jy = 1E-26 Ws/m² to measure them. For example, our Sun at 10 GHz has a flux of about 4000000 Jy = 4 MJy, which makes it the brightest natural object in the sky.
• with our receiver we measure the power density P picked up by the antenna. This power density can be compared with the thermal noise produced by a resistor of a given temperature T, which is simply P_noise = k * T with Boltzmann's constant k = 1.38 E-23 Ws/K.
• For instance, a resistor at room temperature (300 K) provides about 4 E-21 Ws (or W/Hz), which can be written as 400000 Jy m² = 0.4 MJy m². This means that if our antenna has a cross section of 1 m² (like our dish), it will receive from the Sun about 2 MJy m², only five times as much as the thermal noise that is present in the electronics of the receiver! So we are talking about a signal-to-noise ratio of only 5 (or 7 dB) ...
• Because of this comparison with the thermal noise it is useful to define the Antenna temperature T_ant by P = k * T_ant as the noise temperature that gives the same amount of power density as the received signal. In our example, the Sun would produce on a 1 m² dish an antenna temperature of T_ant = 1156 K
• But please keep in mind that while the concept of the antenna temperature is useful for the technical side of reception of signal, it is not related to the properties of the source.

• A somewhat more abstract, but more revealing quantity is the Intensity (or specific intensity or surface brightness) I of the radiation: this is the power per unit frequency interval passing through a surface of unit area and from (or into) a cone of unit solid angle. The solid angle Ω measures the fraction of the entire sky which is covered by the source, the whole sky having a solid angle of 4π. The unit of the intensity is W/Hz/m²/sr ... where sr stands for "steradian" and means: per unit solid angle.
• For a small circular source, one can compute the solid angle as Ω = (angular diameter * π/180°)² π/4 which is often given by this approximate formula: Ω = (angular diameter * π/180°)²
• is the source much larger than the antenna beam, so its radiation fills the entire beam, the relevant solid angle is that of the antenna itself: Ω = Ω_ant = λ²/A This relation between the solid angle and the effective cross section of the antenna holds for all antennas.
• Flux and intensity are related by F = I * Ω
• The intensity has a very important and useful property: along a line of sight in vacuum it does not change, irrespective of the distance from the light source. It changes only, if there are additional light sources or if light is absorbed by intervening material. Thus, the intensity tells us about the nature of the light source.
• Please note: the intensity (or surface brightness) of a source is independent of its distance, but the flux received from it decreases with the square of the distance! Put in other terms: a square arcsec of a solar-type star in a far away galaxy is as bright as a square arcsec of our Sun nearby!
• Another useful property is that the intensity of body emitting thermal radiation - this is a good approximation for the Sun and many other bodies, such as our bodies! - is reasonably well described by the black body law (or Planck curve): I = B = 2 h f**3 /c² / (exp(hf/kT) - 1)
• Since the frequencies of the radio range are comparatively low, so that one may use the Rayleigh-Jeans approximation instead: I = B = 2 k T /λ² which means that the intensity is directly proportional to the temperature of a body!
• in radio astronomy it is useful to define the Brightness Temperature I = 2 k T_B /λ² irrespective of the origin of the radiation. But for thermal emission, the brightness temperature is equal to the temperature of the emitting body, thus it tells about the internal physics of the source.
• If we measure intensity in Jy/sr, the above formula for the brightness temperature becomes I = 2760 T_B/λ² with the λ in meter.

| Top of the Page | Back to the MainPage | to my HomePage |

last update: Apr. 2013 J.Köppen