Basic Data Reduction
Joachim Köppen Strasbourg 2007
Please consult also: Solar Observations
and Lunar Observations which contain hints for
data reduction under more difficult conditions.
Since in radio astronomy we observe signal close to the noise, we need to reduce
carefully the raw data, before we can really use and interpret it. What needs to
be done is this
- our data is in units of dBµV, a logarithmic measure of the power, relative
to a signal of 1µV at the receiver's input terminal: dBµV
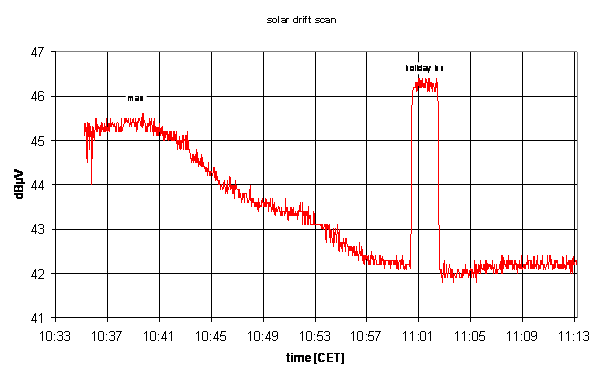
- we first need to convert into a linear measure of power, by applying
to all data
datum = 10**( dBµV / 10)
- next, we determine the background power level, by averaging over a
sufficiently long stretch of data obtained in the empty sky:
background
of course, this is already in linear units!
- in the same way, we determine the level of the calibration, from
the pointings on the Holiday Inn:
calibration
- now we can reduce all data, by subtracting the background and
calibrate the data to the power of the calibration:
power = (raw_datum - background)/(calibration - background)
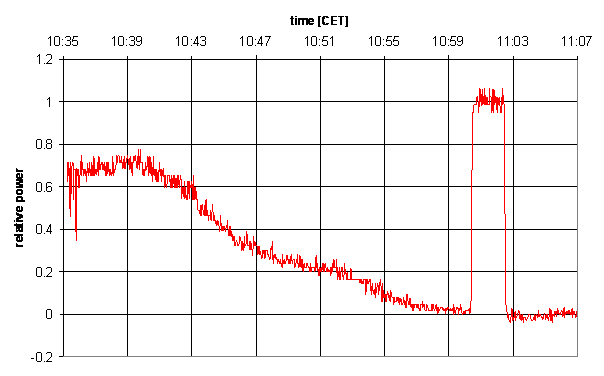
- often the fluctuations in the curve are still rather large. So one
could apply a smoothing of the data by averaging over a number of data
points. This was done here:
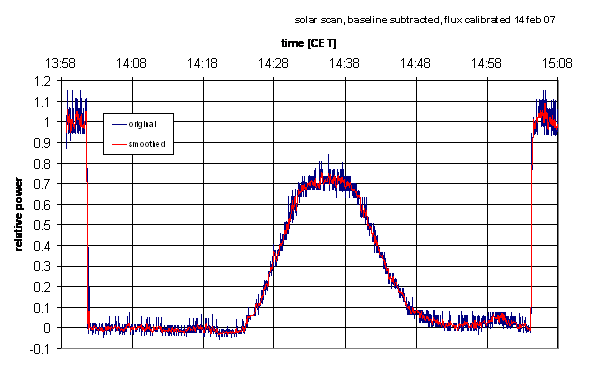
- if we multiply with the temperature of the calibrator, we get the
Antenna temperatures
T_ant = power * 300 K
- if the background and/or the calibrator levels change with time,
one could apply a linear interpolation of these levels between the
initial and final values ... but sometimes these variations do not seem
to follow such a simple time dependence. Thus, the only thing one can
do is to take constant values for background and/or calibration, and
simply accept that the antenna temperature can have excursions into
negative values ... Analysis may be tricky, but that's reality of
doing observations!
If you want to interpret data of the Moon or the Sun, you also need two more data
which you'll get from the prediction applet:
- If you want to convert the times into angular degrees, for instance
when you want to get from a full drift scan the antenna pattern in
true degrees, you need to know the speed with which the sun crosses
the sky. This is close to 15 degrees per hour (360 degrees per day!
or 1° in 4 minutes) ... but only when the Sun is located on the
celestial equator, i.e. on 21 march and 21 september. For any other
times, the angular speed is somewhat less. It depends on the actual
Declination δ of the Sun or Moon (be sure you don't
confuse with the Elevation angle!). We apply this formula:
angular speed = 15°/hour * cos(Declination)
Since in winter and in summer the Sun will be at declinations as much
as -27° and +27°, respectively, the angular speed can be as low as
13.3°/hour!
- the angular diameter. This is necessary for conversion of the
antenna temperature into true surface temperature:
T_surface = T_ant * (antenna HPBW/angular diameter)²
This factor arises because the Sun has an angular size less than the
HPBW, so its radiation does not fill the antenna beam completely, but
the calibrator signal does it. Hence to give the same received power,
i.e. same antenna temperature, the Sun must be correspondingly hotter.
| Top of the Page
| Back to the MainPage
| to my HomePage
|
last update: May 2013 J.Köppen





