If we had eyes to look at the sky in the light of the 21 cm line of neutral hydrogen we would see like in the all-sky image below (from National Radio Astronomy Observatory / Associated Universities, Inc. / National Science Foundation) that the emission in strongly concentrated along the great circle of the Milky Way: The hydrogen gas is essentially found in the Galactic Plane.
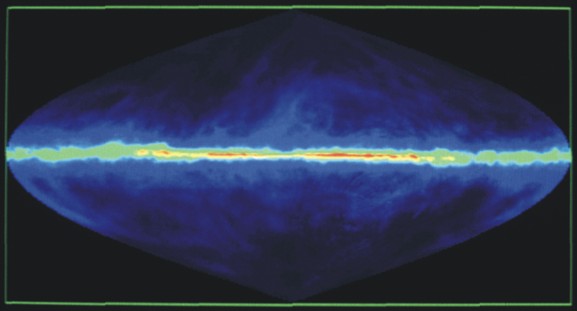
The gas disc is substantially thinner than the disc in which the stars are located. From the above false-colour image we also get the impression that the thickness is not the same in all directions. For example, towards the Galactic Centre - in the centre of the image - it looks thinner than in the direction of the anti-centre. Let us measure the thickness of the gas disc, and find out more about the gas in our own Galaxy. Below we describe how to do it as a workshop activity:
Objectives:
- Become familiar with using a radio telescope
- Understand how radio observations can teach us about our Galaxy
- Derive the thickness of the Milky Way’s gaseous disc
- ESA-Haystack Radio Telescope
- Computer with JKSRT3 software to operate the radio telescope
- Computer with Microsoft Excel for the analysis
Observational Procedures
Once you started up the system, as described here you
are ready to observe. Here we will expose you to two different types of
observation. First it is important to try the manual version. It is good to know
what you are looking for
and you will get a real feeling of what it is like to use a telescope. We hope
that seeing how easy it is to use will motivate you to do some of your own
observing. We also want to provide some hints on what you should be looking for
while you’re observing. First, watch the waterfall plot. The variation you see
between each line should be slight and is due to the fluctuations of the noise in
the signal. You may click on the yellow fields to adjust the range of the values
represented by the colours. Since the galactic emission is concentrated to a
narrow frequency range, you should be able to discern eventually a vertical band
of slightly higher signal. This is also seen in the frequency plot to the upper
left: the black curve shows the current spectrum, the red curve is the accumulated
one, so that after a while the galactic features would become more distinct.
After you had tried the manual observing, we will encourage you to run batch files
while you are in class or doing other things. This will allow for much easier,
less tedious data acquisition and hopefully permits you to accumulate as much
data as you may need.
Manual Observations:
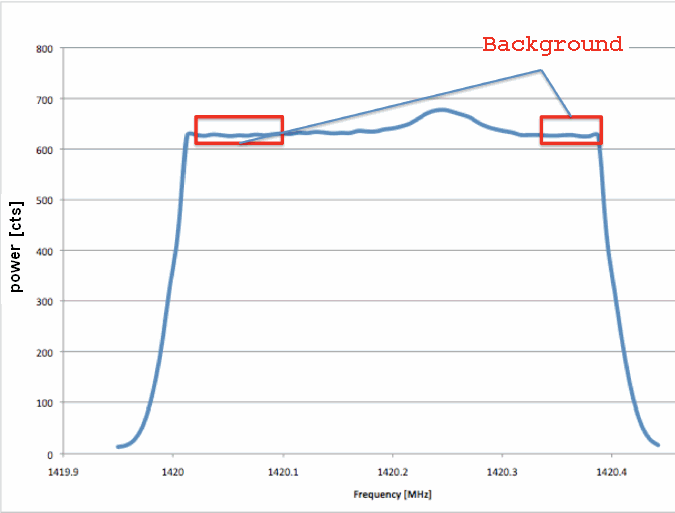
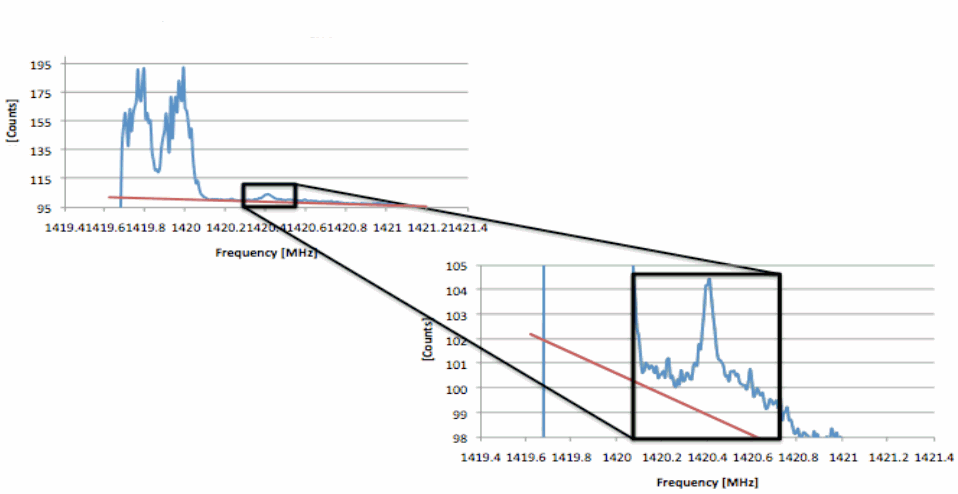
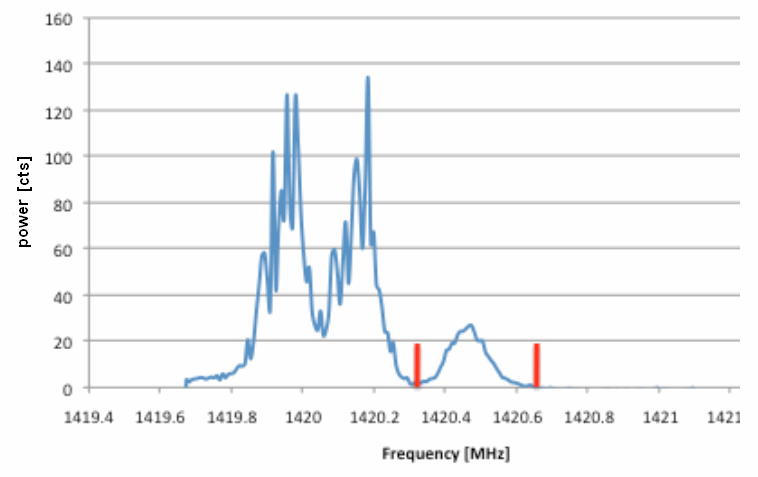
Analysis
Treatment of Each Latitude
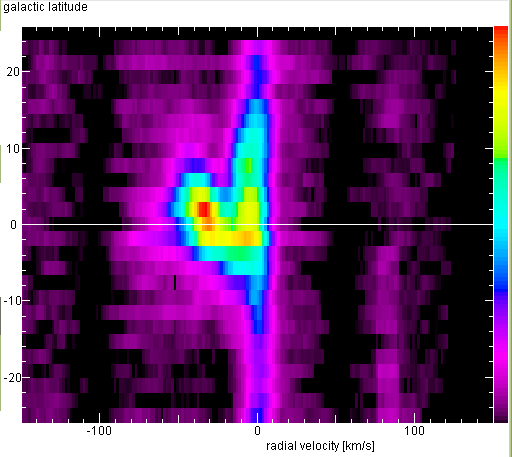
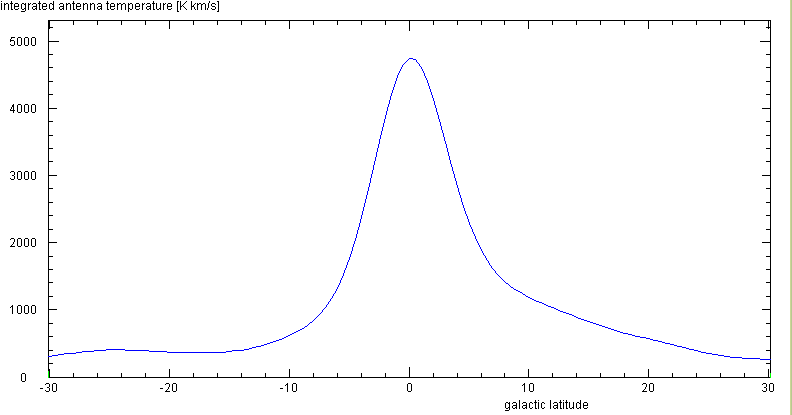
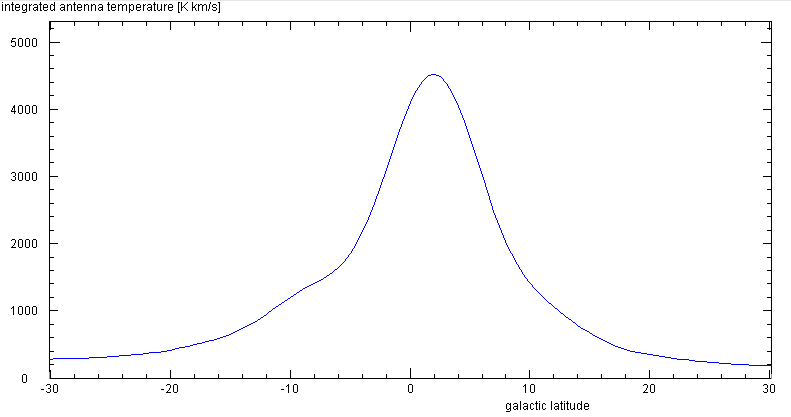
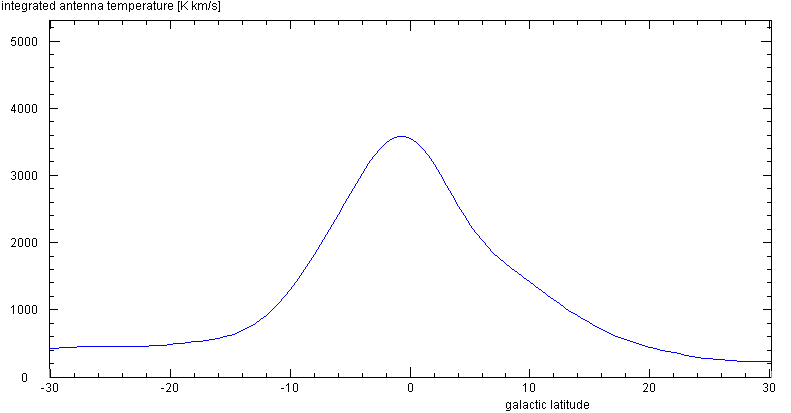
From the Leiden/Dwingeloo Survey of the HI disc - done with a 25 m diameter radio
telescope - one obtains these vertical profiles, after degrading the angular
resolution to 6°, the HPBW of our telescope: l=20°
90°
150°
and 180°
Interpretation and Modeling
We may interpret the obtained vertical profiles in various ways:
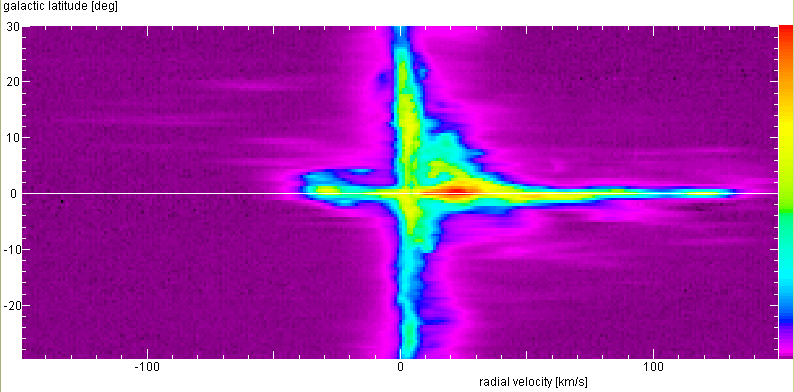
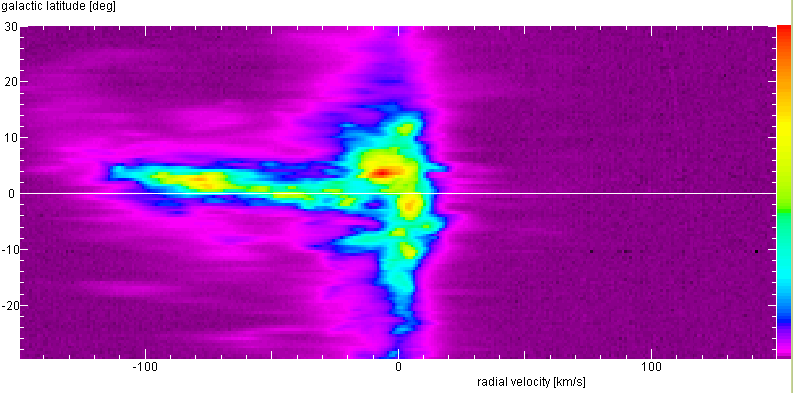
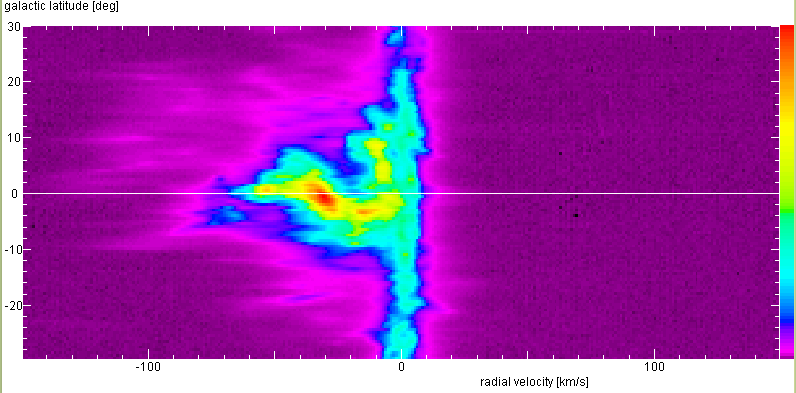
Latitude-Velocity Diagrams
When making the vertical profiles, we throw away the information from the radial
velocities. Since the frequency of a feature in the spectrum relates to the radial
speed with with this packet of gas moves away from us or moves towards us, we can
learn also something about how the gas motions in the disc: The easiest way is to
make a map - similar to the waterfall plot:
90°
150°
and 180°
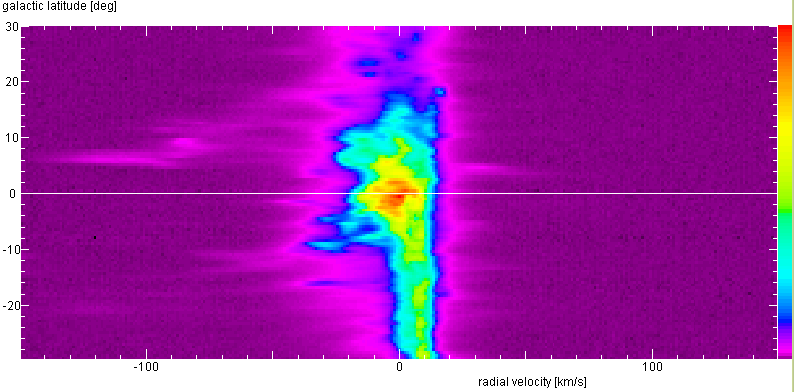
The white horizontal line marks the Galactic Plane. Our plots cannot show structures as
fine or as faint as these, but the essential features will be there! What do they mean?
| Top of the Page
| Back to the MainPage
| to my HomePage
|
last update: Feb. 2010 J.Köppen
Batch Observations:
Basic Operations
Modelling tool for the Galactic Disc
Below are the latitude-velocity maps from the original Leiden/Dwingeloo Survey data,
for l=20°