
The distance from a point in direction α and far away to a point x on the aperture will be shorter than to the centre of the dish, by the amount of x sin(α). Thus the wave of wavelength λ emitted from the centre arrives a little later (by x sin(α)/c) than the wave sent off from point x. The two waves have a phase difference of 2πx sin(α)/λ, and depending on this difference they will interfere more constructively or destructively.
The result of integrating over all contributions from all parts of the aperture is that the amplitude of the electric field is simply the Fourier transform of the aperture's illumination.
It is straightforward to compute the radiation pattern for a uniformly illuminated aperture:

The sinc(x) = sin(x)/x function is the Fourier transform of a rectangular pulse, which appears in various other problems ...
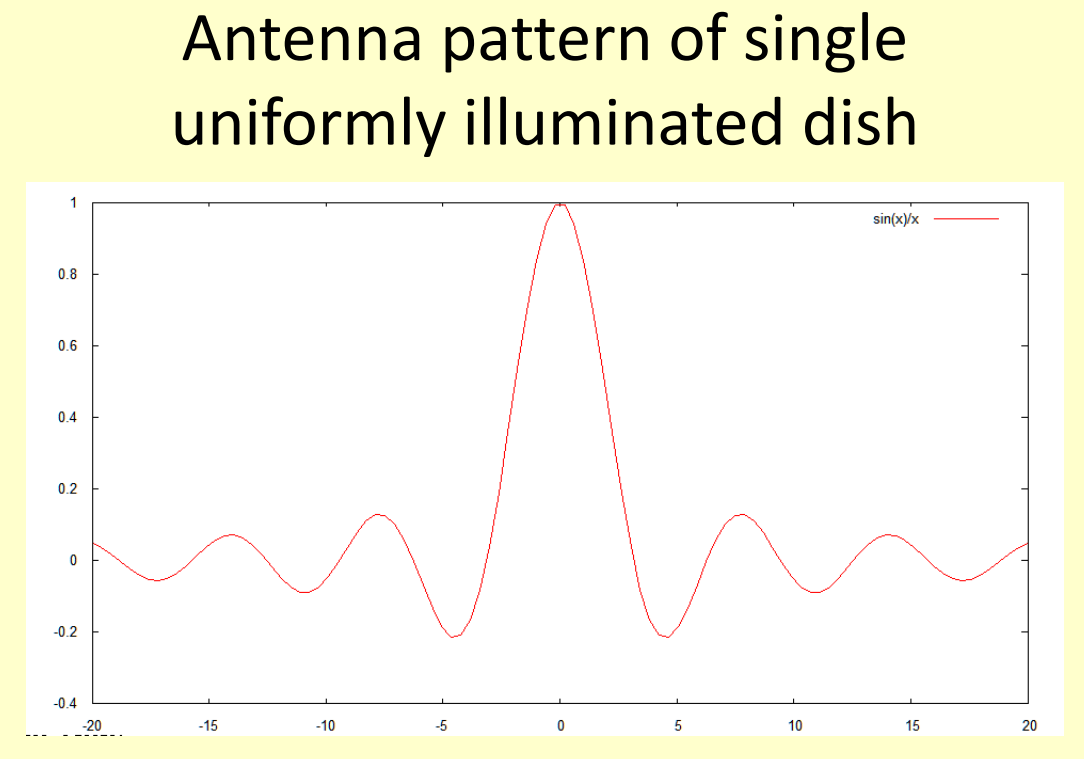
The plot of the amplitude shows that around the central maximum - which we call the main lobe of the antenna pattern - there are numerous lower maxima - which are called the side lobes, with positions of zero intensity or zero sensitivity in a receiving antenna.
Note that the angular width of the main lobe decreases with D/λ, so that a wider aperture gives a narrower antenna beam, which is the characteristic feature of the Fourier transform!
The radiation pattern of a circular aperture is very similar, because the sin(x) is replaced by the Bessel function J1(x).
| Top of the Page | Interferometer Explorer | JavaScript Index | my HomePage |