How to deal with impacting bodies
Joachim Köppen Kiel/Strasbourg/Illkirch February 2002
Contents
The DecisionMap Applet gives rough estimates for the warning time and the energy necessary to make a deflection of an approaching body. It computes them in a straight-line approximation, neglecting the effects of the gravitational fields of the Sun and the Earth, but taking into account that the Earth moves with respect to the Sun with about 30 km/s.
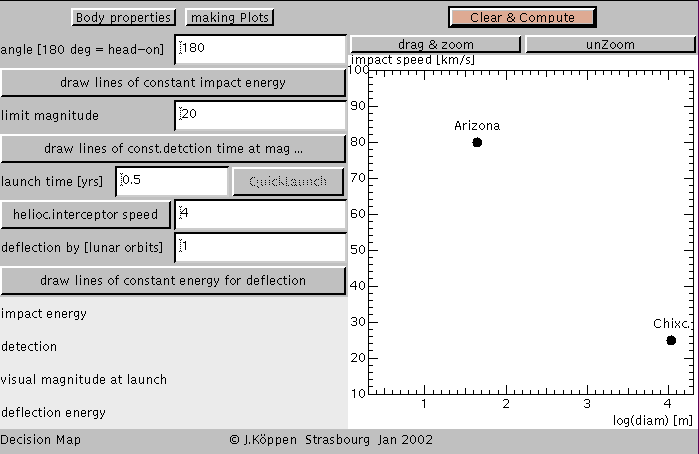
When you start up the applet, you hit the Click to Start button, and you see something like the following screen:

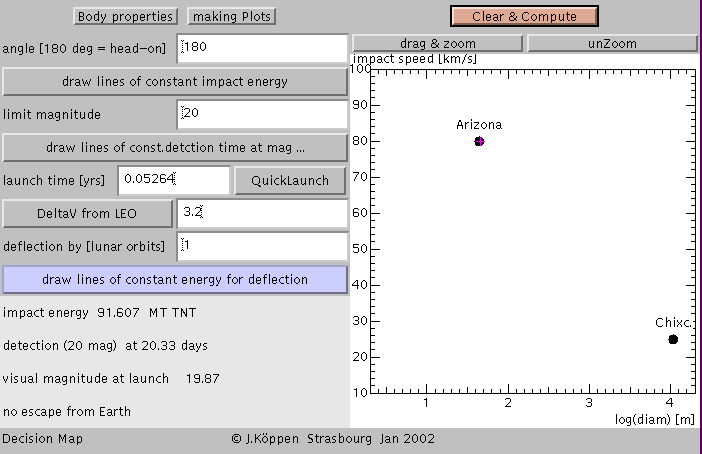
The value of the approach angle is 180 degrees, which means that
the asteroid is on a head-on collision course with Earth.
To change this angle, click the text field, enter a new value, and
hit the Enter or
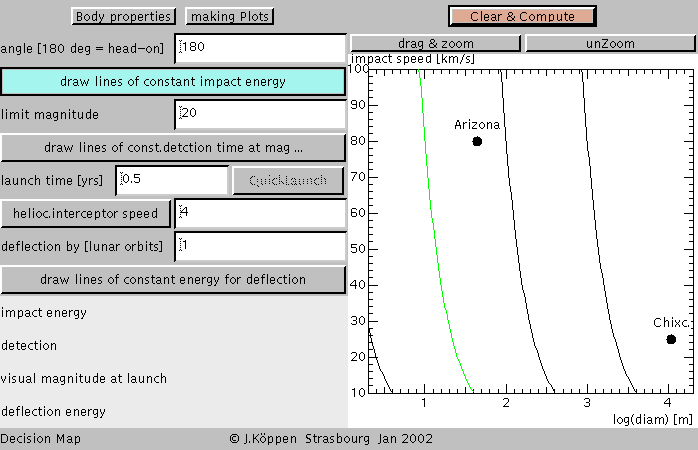
To show the lines of constant impact energy, one clicks on
the appropriate large button, which will then change its
colour, and then the "Clear & Compute" button. One gets
from left to right 1 kT,
1 MT (green), 1 GT, and 1000 GT = 1 TT (Tera-tons).
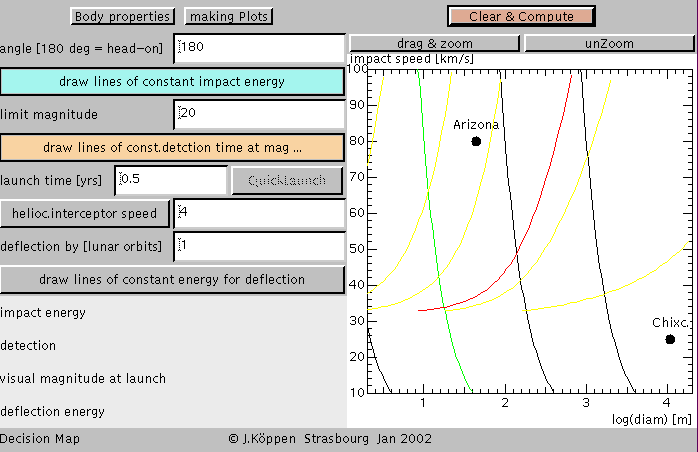
Adding the lines of constant detection time (at a visual
brightness of 20 magnitudes). Note that this calculation
takes more computing time.
From left to right there are shown:
1 day, 1 week, 1 month, 0.5 years (red), 1 year, and 10 years
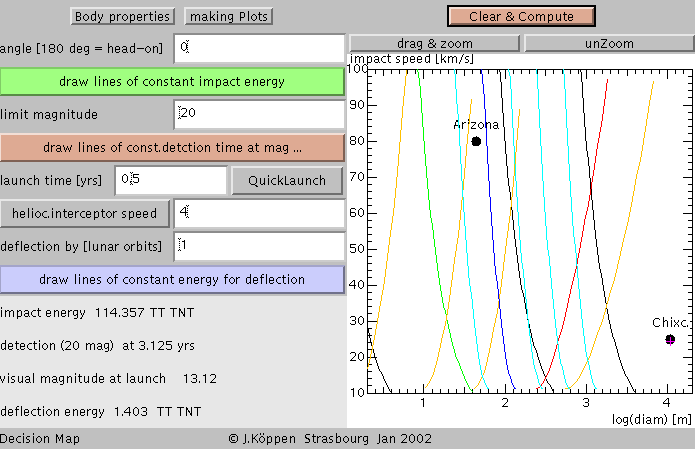
Switch off the previous lines by clicking the buttons, and
clicking the bottom button. This draws the curves of constant
energy necessary for a deflection by 1 lunar orbit radius
if we send an interceptor 0.5 years before impact and
at a speed of 4 km/s. The curves from left to right refer
to 100 kT, 1 MT (blue), 10 MT, 100 MT, and 1GT.
This is the change of kinetic energy necessary for the
deflection, but the actual energy by impact or by a
nuclear explosion must be higher, corresponding to
a certain efficiency factor.
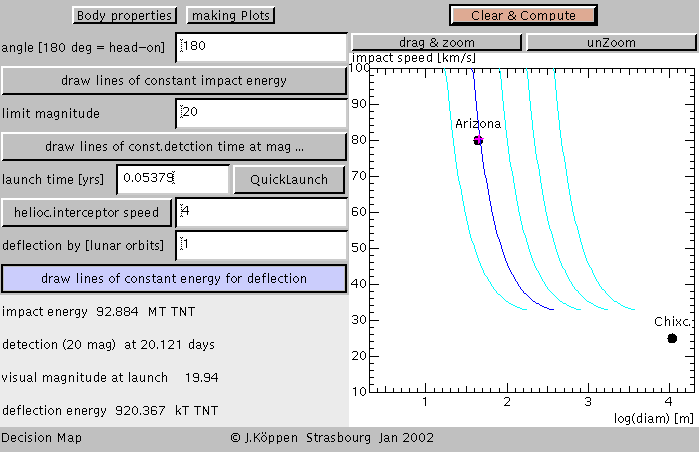
To get the next screen,
we have simply clicked with the mouse on the black
dot, representing probably the asteroid which caused the
crater in Arizona, which gives us in the lower left the
impact energy, detection time. Then we clicked the
button "QuickLaunch" which means that we launch the
interceptor right at detection time, and we
clicked the Clear & Compute button to redraw the
plot. Finally we clicked again on the Arizona locus to
get the numerical value for the deflection energy using
such an early interceptor:
You'll notice that the curves do not go below a certain
velocity: for a head-on collision course there is a minimum
impact velocity of about 32 km/s, if a body with no velocity
w.r.t. the Sun collides with the Earth, which comes in at
its orbital speed of 30 km/s. When you click the mouse
in this forbidden area, you also get the appropriate
mesage.
Clicking on the button "helioc.interceptor speed" changes
over to the "DeltaV from LEO". This means that any entry
to the textfield is now being interpreted as the velocity
change for the interceptor being launched from a Low
Earth parking Orbit. If this entry is too small, you'll be
told that it can't escape from Earth orbit, and there will
be no blue curves when you request their drawing.
There is something about the conversion of heliocentric speed
into DeltaV from LEO which you might find most puzzling:
For an approach angle of 180 degrees, enter a helioc. speed
smaller than about 30 km/s, say 4 km/s. Clicking the button
changes over to show a DeltaV of 26 km/s. Clicking again
does not bring back the original 4 km/s but 56 km/s. What's
wrong? There is a simple reason: launching the interceptor
from LEO with 26 km/s, we could send it in the same direction
of the Earth's movement around the Sun giving a heliocentric
speed of 56 km/s. But also, we could send it in the other
direction giving only 4 km/s, still towards the asteroid!
You'll notice that the deflection energy also changes.
(mathematically speaking, the conversion from LEO speed
to heliocentric speed has two solutions, while the inverse
conversion has one). Both approaches could be used,
but obviously the faster approach is to be preferred.
If you wish to insist on the slower approach, you may do so
by entering the heliocentric speed.
Giving the heliocentric speed is useful for comparison with
the orbital speed of the asteroid, e.g. from the other applets.
For the Chicxulub crater the head-on collision does not work:
the approach from behind does. Here is the complete
plot for this situation: one would have had a 3 year
warning time, but a deflection would have necessitated
a lot of energy!
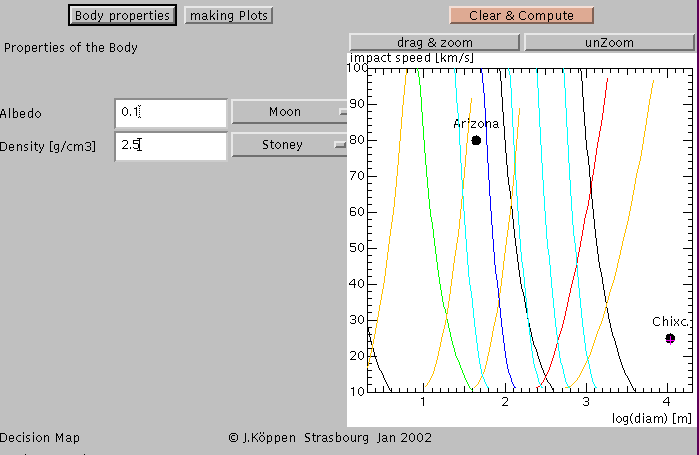
There is also a page to alter the albedo and the
density of the asteroid
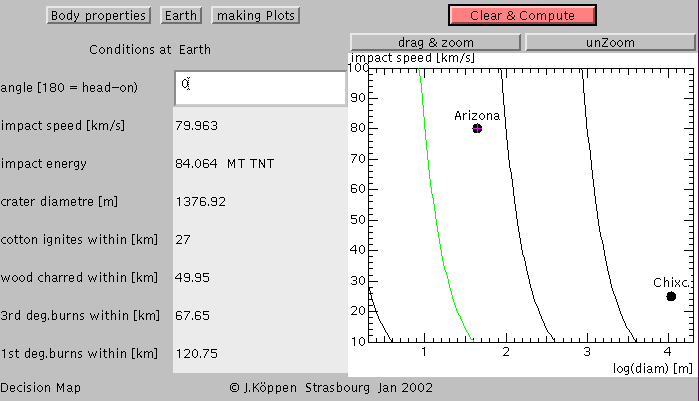
as well as a page which gives the estimates for the resulting
crater size and measures of the devastation from the impact.
The formulae are taken from the
JavaScript utility by A.Goddard based on formulae
by Eugene Shoemaker.
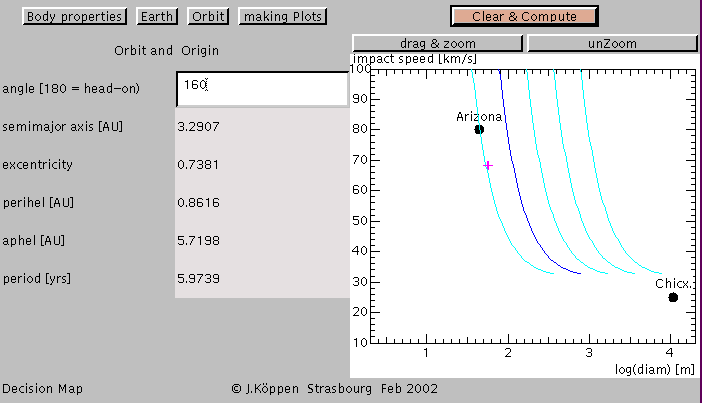
Another page shows for each mouse click on a situation
the orbital parameters of the body, the semimajor axis,
the eccentricity, aphelion and perihelion, and the period.
This allows to judge which could have been the origin of
a body, for instance an asteroid crashing into Earth with almost
70 km/s and almost head-on (160 degree direction) could have
been deflected from an orbit just outside Jupiter's orbit into a
rather elliptic orbit (eccentricty 73 percent):
By clicking in the plot, one can verify that bodies with impact speeds
larger than 72 km/s would need to be head-on crashes with bodies
on hyperbolic orbits, while anything with less than 60 km/s
must have come from inside the Earth orbit.
On the other hand, all collisions "from behind" with speeds larger
than 17 km/s are due to bodies on hyperbolic orbits, and bodies on
elliptic give impact speeds between 11.5 and 17 km/s.
| Top of the Page
| Controls
| Applet
| Applet Index
|

The controls: