Response of Test Particle in a Potential
Subjected to an External Force Pulse
Joachim Köppen Kiel Nov 2017

Some brief explanations

Some insight in the mechanism of the removal of gas from the disk of a spiral galaxy by ram pressure stripping can be gained by considering the movement of stars or parcels of gas perpendicular to the galactic plane, which follows the perturbation by a pulse of an external force. This is explored in the simulation.

Consider a parcel of gas at some galactocentric radius, and let the parcel be represented by a test particle (a mass point) which sits in the gravitational potential caused by the stars and gas of the galaxy. Let us regard only the motion perpendicular to the galactic plane. Then the potential as a function of height z above the plane has the characteristic form of a well of some finite depth, for instance Φ(z) = - v_esc²/2 /(1+z²). It is convenient to use normalized units: Let us set v_esc = 1 so that all velocities are measured in terms of the escape speed from the galactic plane. Furthermore, z is given in terms of the scaleheight of the vertical potential.

Initially, the particle is at rest in the galactic plane z=0. It shall have unity mass. For small deviations from the rest position, the particle will experience a restoring force, which increases linearly with the deviation. If it is given an initial velocity v_z(0) or it is perturbed, it will perform small amplitude oscillations around its rest position. The length of one period is 2π in the normalized units.

The action of the ram pressure is described by a pulse of an additional force with specified strength and duration: F(t) = F0 f(t). Then the particle will move according to its equation of motion: d²z/dt² = Φ(z) + F(t)
This equation is solved numerically using a 4th order symplectic method. Thus the momentum is conserved with machine accuracy.

The controls of the simulator are:

• Potential: The user may choose between three potentials: a parabolic well, a Gaussian well, and a hyperbolic secans well. For comparison the harmonic oscillator is included, from which the particle cannot escape.
• Pulse of external force: can have the shape of a Gauss or a Lorentz profile (with different time constants before and after the peak force), a simple Tophat pulse, or a step-up function with a certain rise time. For each pulse shape, the peak force F0 and the necessary time constants can be entered.
• Initial conditions of the particle: The user may specify the initial position z and velocity vz. The latter is in units of the escape speed from z=0.

• Modelling: The user specifies the maximum time of the simulation run, and the time step for the numerical computation. The latter determines the accuracy of the results. A smaller time step gives more accurate results, but takes longer!
• start, stop, resume: these buttons operate the simulator. During calculations the stop button shines red.
• autoClear: if this button is active (green), the plot is always cleared when another model is computed. If one wants to superpose plots from models with different parameters, such as the peak force F0, click on the button to make it inactive. Thus, one can make plots which compare different models.
• X = and Y = : the abscissa and ordinate of the plot can be chosen from these parameters:
  • time: with respect to the peak force. The simulation always starts about 6 time scales before the moment of maximum force.
  • position z
  • velocity vz (in units of v_esc)
  • total energy (in units of v_esc²)
  • the potential (in units of v_esc²)
  • pulse force
  • restoring force
  • net force = pulse force - restoring force
  • available momentum = time integral of the pulse force
  • received momentum = momentum deposited in the particle
  • momentum efficiency = received mom./available mom.
• Set range: when this radio button is clicked, the plotting limits are taken from the associated fields (min, max)
• Mouse position: displays the coordinates of the present position of the mouse.


• After entering a new number in one of the fields, hit the Enter key to start another model calculation.
  The colour of the plotted curve indicates whether the particle is bound (blue) or has achieved positive total energy and escapes (red).
  In the z - vz plot a green curve, labelled by E=0, indicates the locus of zero total energy.
  Magenta lines mark the height z_max where the restoring force has its maximum value.


• Results: After each model computation, the time and the position z of the escape are displayed, i.e. when the total energy becomes 0. Also shown are the total momentum available by the force pulse (the time integral over its force) and the momentum deposited in the particle.

• Short pulse limit: If the pulse is shorter than the period for vertical oscillations, the particle receives all the momentum from the pulse, which is equal to the time-integrated force of the pulse, while still at rest position. It will then execute oscillations whose amplitude depends on the acquired momentum. If the momentum exceeds some limit, the particle can escape.
• Long pulse limit: If the external force lasts longer than the period for vertical oscillations, e.g. for a constant force, the particle is pushed away from its rest position. For a small force it will come to rest at some height above the plane where the local restoring force just balances the external force. If the force exceeds the maximum restoring force, the particle is pushed beyond that height, and with the force continuing long enough, it may achieve a positive total energy and will escape. This is what is at work in the criterion by Gunn & Gott (1972) for ram pressure stripping.

Sample plots

Blue curves indicate that the particle is bound in the potential, red curves show that it has reached positive total energy and is escaping. A green curve, labelled by E=0, indicates the locus of zero total energy. Magenta lines mark the height z_max where the restoring force has its maximum value.

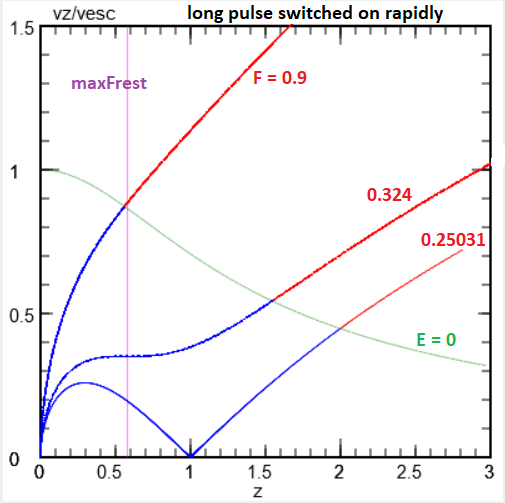The Long Pulse Limit: reponse to a constant external force: For the parabolic potential well the restoring force has its maximum value of 0.3247 at a height zmax=0.577, where the potential energy is still negative -0.375. Thus, if the particle is pushed with a force equal to or greater than this maximum value, the particle can be brought up well beyond that height but it remains bound in the well. Thus more work has to be done by the force to liberate the particle from the potential. If we push the particle with a force of 0.324, the value of the maximum restoring force, it reaches that height zmax with a speed of 0.347, but its kinetic energy of 0.12 is still insufficient to overcome the potential energy. Since the force continues at a constant level, the particle achieves escape speed at time = 4.78 at a height of 1.55, well above the height for maximum restoring force. However, the particle can already be detached by a somewhat lower force: the minimum force necessary for the particle's escape is 0.25. Here, the particle passes zmax with a speed of 0.19, which decreases to nearly zero at z=1. If it can pass this critical point, it will eventually be reaccelerated to escape speed at a height of 2 at time=20. If the force level is much higher, escape occurs earlier and at lower heights. For F=0.9 this happens at the height of maximum restoring force at time 1.2, i.e. one sixth of the period for vertical oscillations.

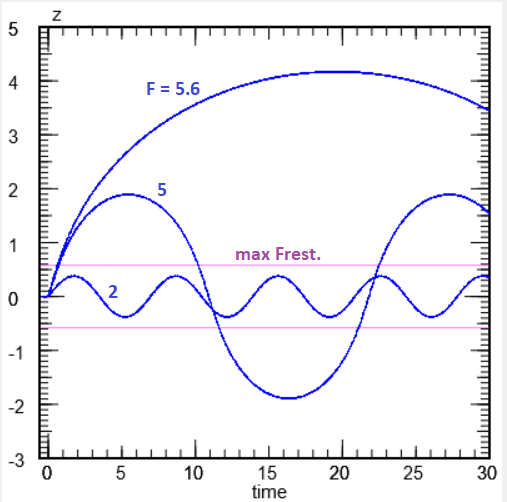The Short Pulse Limit: reponse to a short and weak external force pulse: The particle sits in the parabolic potential well, where the restoring force attains its maximum value of 0.324 at a height zmax=0.56. A Gaussian pulse of force with a time scale of 0.1 (i.e. FWHM=0.17) is applied. As long as the peak force of the very short pulse does not exceed 5.7, it kicks the particle into oscillations about its rest position at the bottom of the potential well. For a peak force of less than about 2, the amplitude is smaller than the height of the maximum restoring force. With a larger force the particle can be kicked into slow oscillations with amplitudes much higher than that height.