Solar Eclipse 2015

Eclipse map and data courtesy of Fred Espenak and Jay Anderson The total solar eclipse on 20 march 2015 had the greatest eclipse in Kiel at 09:46 UT and the Sun was covered by about 80 percent. First contact occurred at 08:38 and last contact at 10:56 UT ...
... but as the high fog arrived right on time, we at DL0SHF, the Radio Observatory and Ground Station in Rönne did not see anything. Fortunately, Hermann Fenger at our 'outstation' in Bielefeld enjoyed a glimps through the clouds and took the visual image at 10:54 UT. Focal length 200 mm, exposure 1/320 s at ISO 100 and f-stop 7.
From the images in visual light by Meteosat received at DL0SHF two movies were compiled: the one on the left shows the entire Earth disk in colour during the entire day. The one on the right shows in greyscale how the penumbra passed over Europe. Click on the image to start the video.
In these images the umbra is too small to be visible, but the penumbra of a few thousand km size.
The original images have 768 by 576 pixels. The registration of a single image takes about 12 min, since every image is read line-by-line. The images, taken every 15 min, are sequenced together in Rönne to form the video.



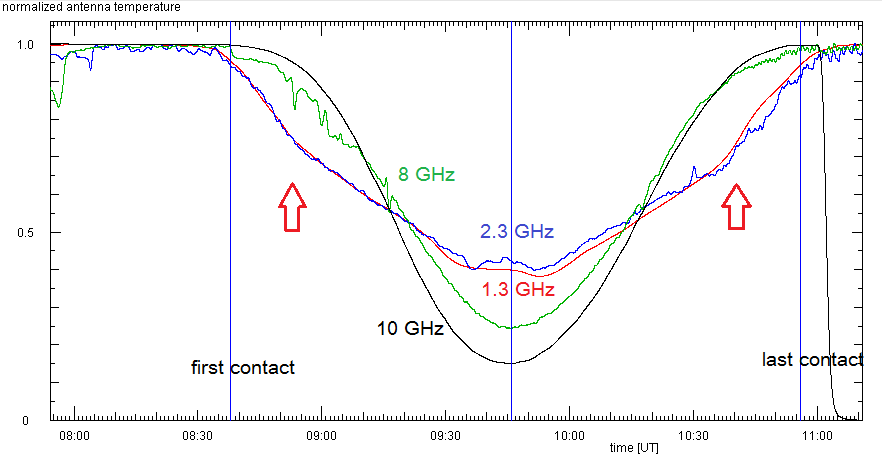
At DL0SHF, we observed entire eclipse on 1.3, 2.3, 8.2, and 10 GHz. The composite plot shows the evolution of the antenna temperatures, normalized to the value before the eclipse. This linear quantity presents the fraction of the solar flux received on each frequency. One notes:
  • at maximum eclipse the signal is lower the higher is the frequency. This is because at higher frequencies the radiation comes from deeper layers, close to the visual 'surface' of the Sun, the photosphere. At low frequencies the emission comes from the corona which extends well above the solar 'surface'.
  • at low frequency the signal starts dropping before it drops at high frequency, and before the first contact in the optical. At frequencies below about 3 GHz the emission comes from the corona, which is the zone of very hot gas which extends above the photosphere and up to a few solar radii. The Moon covers parts of this region before it touches the solar disk.
  • at 10 GHz the curve is shaped like a 'V' while at 1.3 GHz it resembles a 'U'
  • at 1.3 and 2.3 GHz the curve has slight kinks (red arrow points at the one after maximum eclipse) where its slope changes somewhat ...
  • also at 1.3 and 2.3 GHz, there are two small dips in the signal near maximum eclipse. That they appear at both frequencies proves that this is not an instrumental effect or defect. Could it be due to a change in the Earth atmosphere, like passing clouds?
Here are the explanations: In the optical and also at 10 GHz the Sun resembles a disk of nearly uniform brightness. In a simple model for the eclipse one obtains a 'V' shaped profile of the flux fraction. In this model the Moon passes in horizontal direction over the Sun. The distance between the centres of their disk is set to give a maximum covering of 80 percent, as it is predicted for Kiel. The signal drops right at the moment of first optical contact, of course!

Here is the RadioEclipse interactive simulator
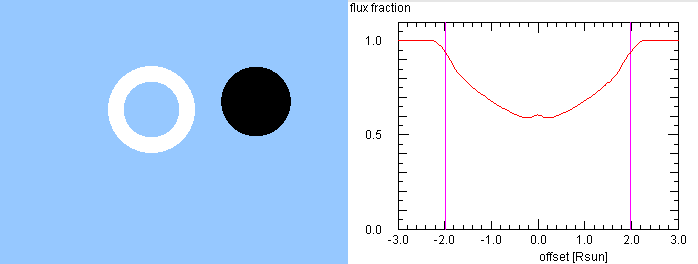
On 1.3 and 2.3 GHz the radio emission comes from the corona, which lies above the photosphere. If we model this with a bright ring, with inner radius 0.8 and outer radius 1.25 (in radii of the optical solar disk) we get:
  • the curve has a shape like a 'U'
  • the signal starts dropping before the first contact (marked by vertical magenta line)
  • at offsets of -1.5 and 1.5 solar disk radii the slope of the curve changes slightly but markedly. This is due to the way the Moon covers the emission ring, which is slightly larger than the Moon
  • at maximum eclipse, there is a slight peak in the signal. This is because the Moon can only cover the inner parts of the coronal emission, but not the outer rim
  • before and after this peak there are slight depressions, just as they are observed on 1.3 and 2.3 GHz. Therefore these dips are not passing clouds, but the consequence of the Moon covering a brighter spot at the Eastern side of the coronal emission.

Here is the detailed Report on Observations, Data Reduction, and first Interpretation ...

... and here: Report on the Modeling of the Observations



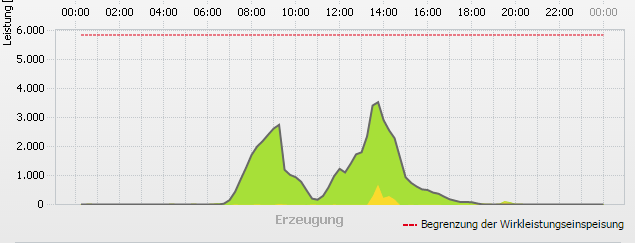
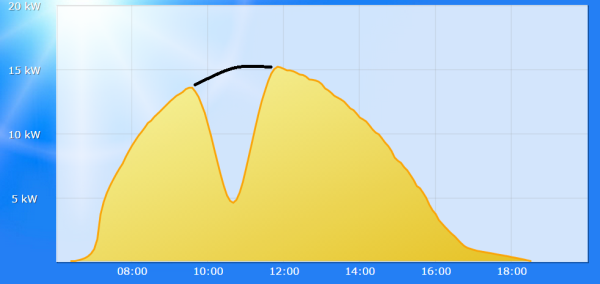
Despite the grey skies in Northern Germany, records from a solar photovoltaic system give solid proof that it did occur here, too ... ;-) A record from Southern Germany allows to deduce the mininum fraction of light to be 31 percent, which agrees well with the 30 percent predicted for this place.

Some Background on the Radio Sun:

Radio emission from the Sun is the long-wave extension of its thermal radiation in the optical and infrared ranges, which is produced by the warm and hot plasma. Apart from a constant 'quiet' component there appears also in times of high activity short or long periods of enhanced radio emission. These are caused by regions of enhanced temperature in higher layers and expelled plasma clouds (CME 'Coronal Mass Ejections').

The layer which from optical observations we could call the surface, is the photosphere with a temperature of about 6000 K. This is the deepest layer accesible to direct observation, since here the density increases strongly with depth, and thus the increasing absorption blocks the view. Above the photosphere, the temerature continues to decrease, to about 4300 K, and then increases again towards the chromosphere, which is only prominent during total solar eclipses due to its emission lines. Above the chromosphere there is the Transition Layer, in which the temperature increases from about 10000 K to several hundred thousand K. Above this extend the Corona up to several solar radii, with very low density and temperatures of millions K.

Since the absorption of the solar plasma incleases towards longer wavelengths, it is not possible in the radio range to look as deep as with visible light. The radiation originates from higher layers the lower is the frequency. At 10 GHz one reaches already only down to the upper chromosphere, below 1 GHz the radiation comes from the Corona. In this way radio observations at different frequencies allow to probe the temperatures in the various layers of the solar atmosphere. Solar radio fluxes are measured several times each day by an international network of radio observatories, and the data are published almost real-time by NOAA. 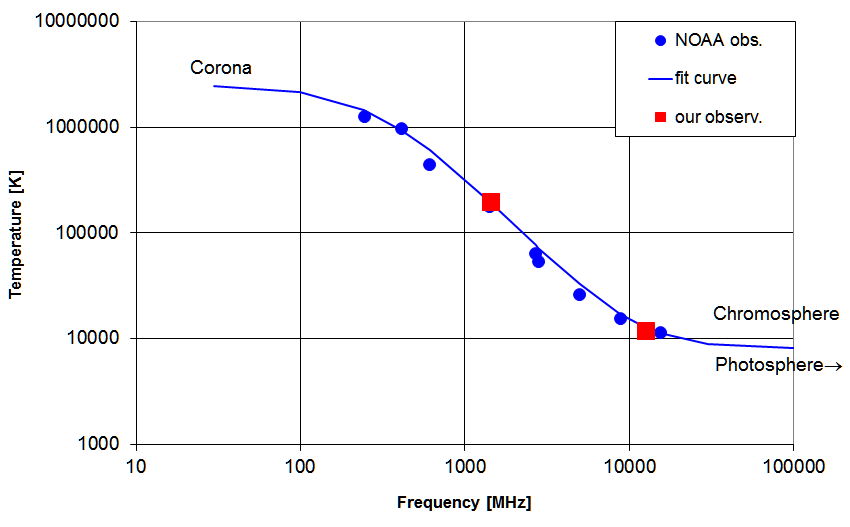The spectral distribution of the radio fluxes

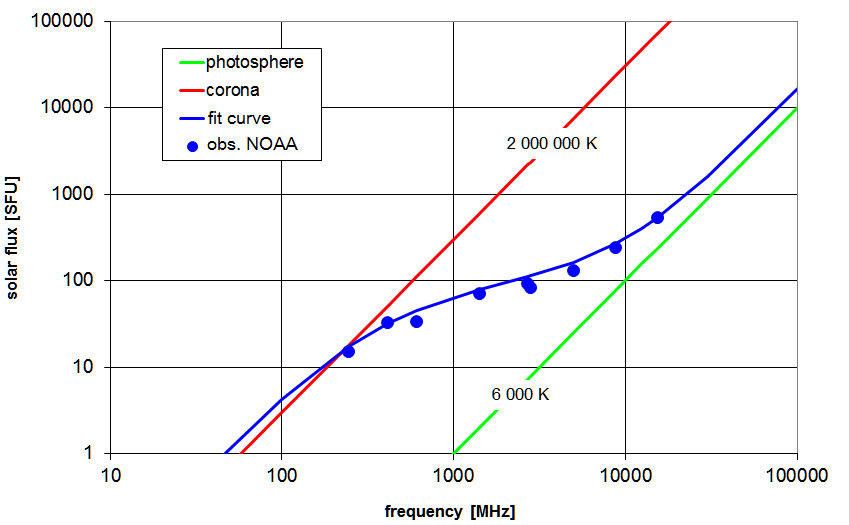
maps the temperature stratification in the solar atmosphere:

Determination the Solar Radio Flux

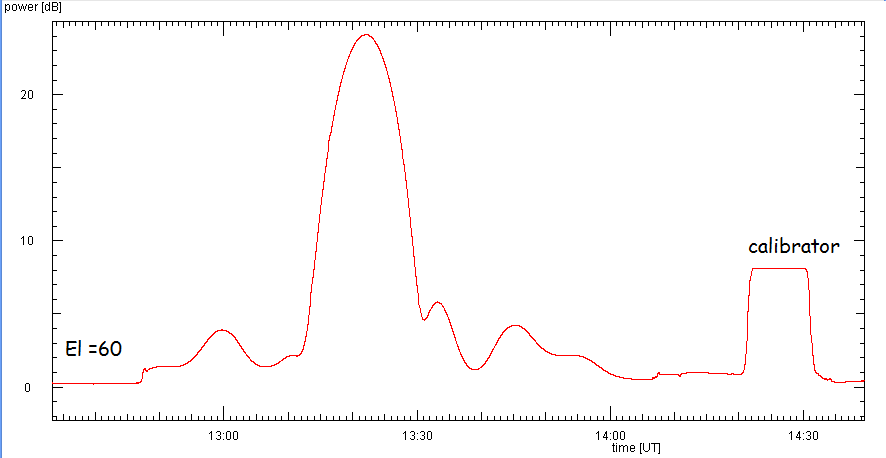
Four measurements are required: All measurements can conveniently obtained by a drift scan: This may look like this observation on 1.3 GHz. The ample time before and after the passage of the Sun allows also to pick up the antenna's weak side lobes.

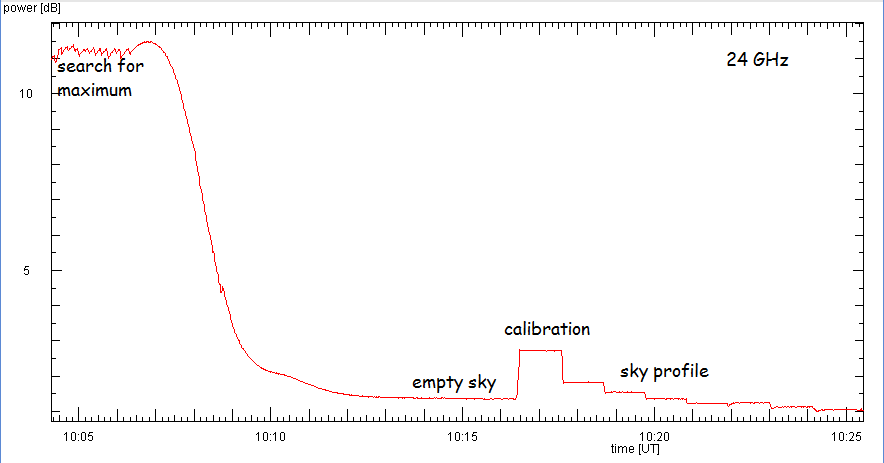
This procedure requires an accurate pointing system. If this is not available, one can first search manually for the maximum signal from the Sun, then with the fixed antenna watch the Sun on its way out of the main lobe. Such a half-scan also yields all necessary information and takes less time:

Interpretation

One follows this procedure: In the fundamental relations for the solar signal (in linear power)
p(sun) = a (Tant(sun) + Tzenit/sinε + Tsys + TCMB)
and for the sky background
psky(ε) = a (Tzenit/sinε + Tsys + TCMB)
one determines the unknown scaling factor a from the flux calibration:
pcal = a (Tcal + Tsys)

Radio Flux

With the knowledge of the effective area Aeff of the antenne the radio flux (in Jansky) is obtained:
Fsun = Aeff/2760 * Tant(sun)

Solar Surface Temperature

The derived antenna temperature is not yet a direct measure of the physical temperatur on the Sun, since it depends on the properties of the antenna:

Half-Power Beam Width

Thus the knowledge of the antenna's beam width is required. As this is an unchanged property of the hardware, a single measurement suffices. It comes free as a by-product of a drift scan: the HPBW (Half-Power Beam Width) is defined as the full width of the antenna's main lobe at half the maximum power. Since in a drift scan the accurate rotation of the Earth provides the horizontal movement of the Sun, one measures the time interval during which the measured (linear) power (above the background) exceeds one half of the maximum. In one hour the Sun at its present declination δsun moves over an angle of 15º cos δsun. Another method is to match the data (red) by a Gaussian profile (blue), as shown below. Here one also notes how well the antenna characteristic resembles a Gaussian function and where it differs. The green line is the level at half maximum power. The black arrows indicate up to where measurements for the main lobe should reach.

| Top of the Page | back to my Home Page |