Three Body Problem: Earth/Moon/Spaceship
Joachim Köppen ... Kiel, Jan 2023

Some brief explanations

This tool simulates the flight of a spaceship in the combined gravitational field of Earth and Moon, which orbit around each other. Since the spaceship has a negligibly small mass, its own gravitation does not influence the other two bodies, which makes this configuration a much simpler version of the complex problem of three gravitationally interacting bodies (such as stars). Thus it is much easier to understand...

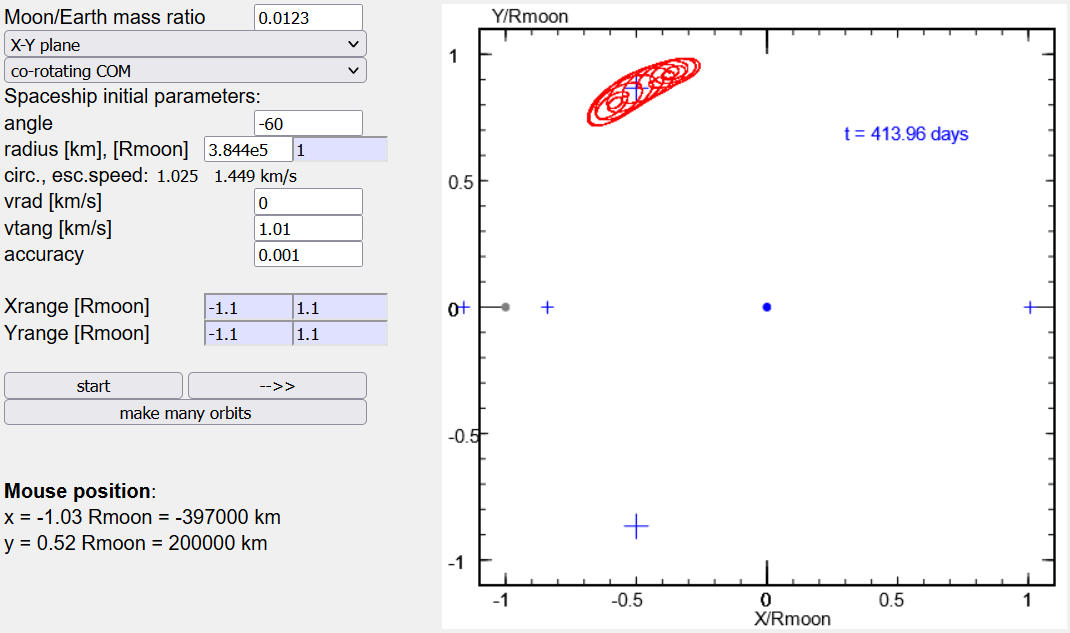
The X-Y-plane shows the situation: the blue dot is the Earth, the grey the Moon, and a red point is the spaceship. The blue plus-signs mark the five Lagrangian points, the larger ones being the stable L4 and L5 (see below).

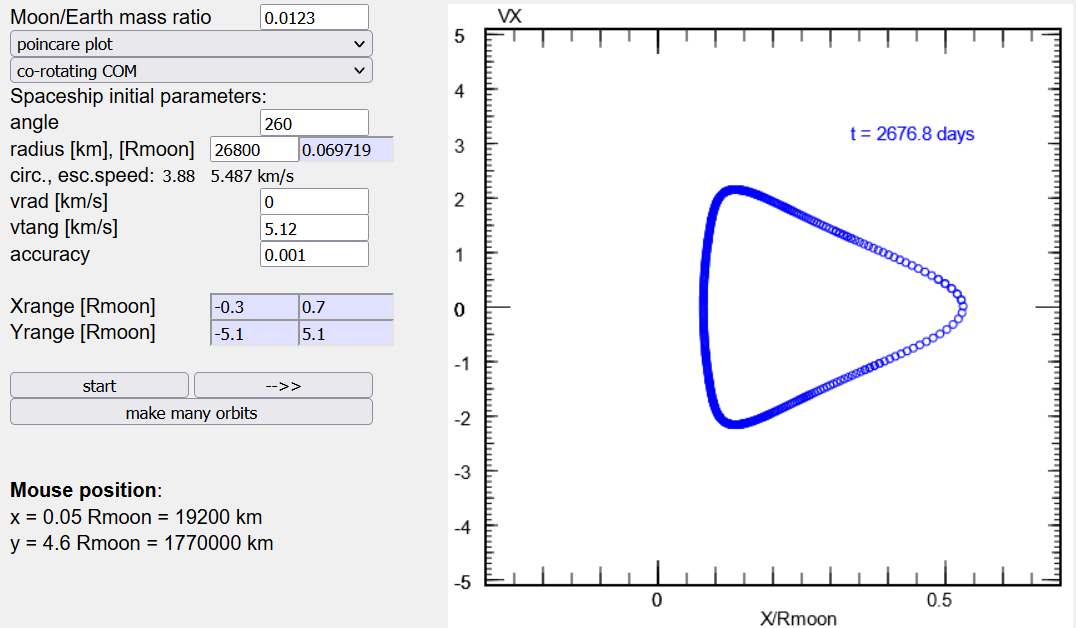
Poincaré map (or surface of section) is an efficient way to inspect the character of orbits: It plots the position X and velocity VX of the spaceship whenever it crosses the Y-axis with positive velocity. See here for a few examples.

While one may choose a coordinate system which is fixed on Earth, or Moon, or the centre-of-mass (COM), it is more convenient to view things from a system which co-rotates with the Moon around the COM, so that Earth and Moon stay at the same place.

The spaceship starts at a radius (in km) from the centre of the Earth, at an angle, (0° is 'right' to the Earth, or at its side away from the Moon; 90° is 'above' the Earth, 180° on its side towards the Moon). The blueish field is in units of the lunar orbit, which may also be used as entry.

The initial velocity of the spaceship is gives as its radial component (note that positive values indicate an outward motion) and its tangential component (a positive value means in the same sense as the lunar motion).

The accuracy parameter may be chosen smaller, if one suspects that the orbit is not accurate enough ...

The plot limits Xrange and Yrange are in units of lunar orbital radius.

Hit the Enter key after changing the value in one of the input fields, to show the new configuration, and put the spaceship to its initial position.

Start: put the spaceship to its initial position.

-->>: the simulation proceeds as long as this button is pressed.

make more orbits: click this button to compute many orbits in a short time.

---

Examples (clicking on a figure opens it in a new page):

If the ship near one of the stable Lagrangian point has an orbital velocity close but not equal to the lunar orbital velocity, it performs a librational movement around one the points:


Poincaré maps:

A regular orbit always makes the crossing at the same point (X,VX).

A rosette-type orbit produces a closed curve

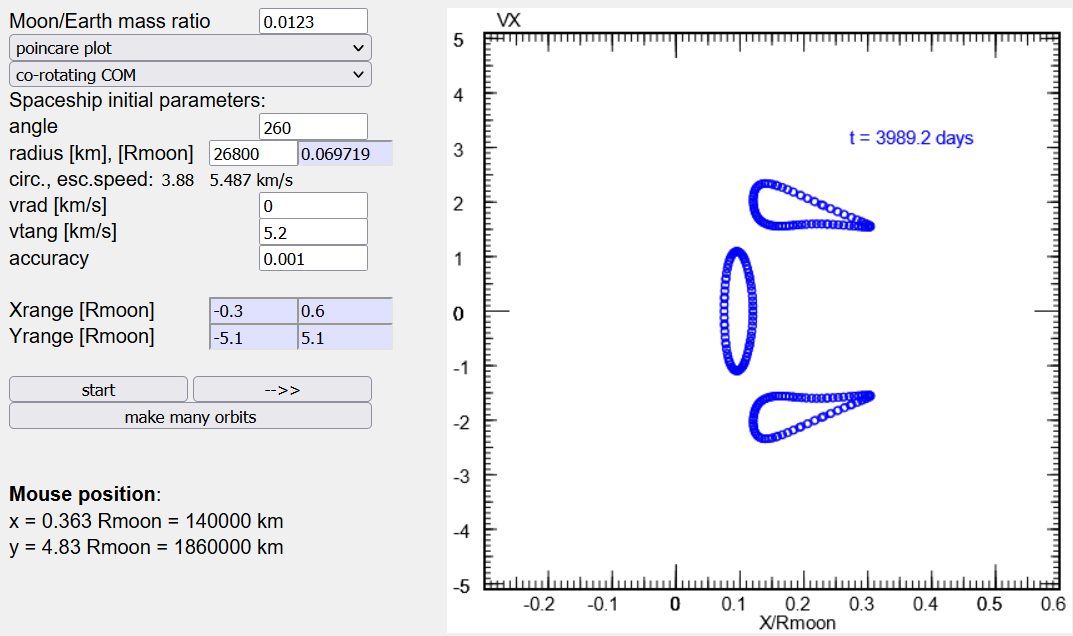
which may also consist of several curves

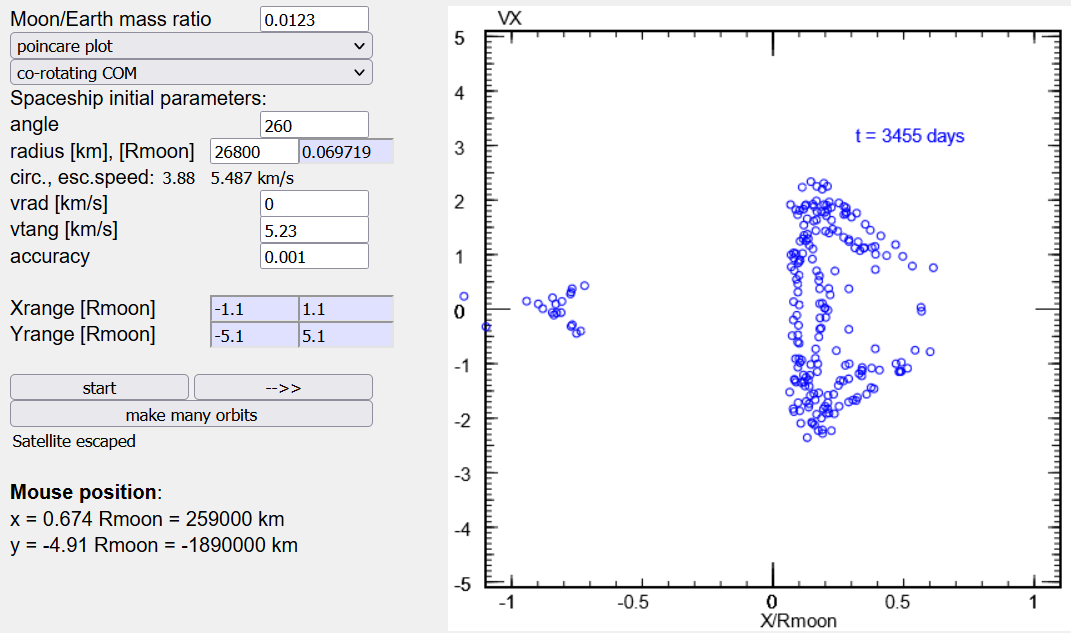
A chaotic trajectory fills an entire area in the (X,VX) plane

---

| JavaScript Index | my HomePage |

---