The Collapse Applet is an extension of the Hydro Applet to compute the evolution of a spherical gas cloud (with its centre at x=0) under its own gravity. See the Help pages of that applet for the basic explanations of the applet.

One principal difference is the spherical geometry which modifies the terms with spatial derivatives. In the applet, we solve the equations not for e.g. the density itself, but for the density times the square of the radius. This preserves the form of the equations.

The other modification is that the gravitational force is an additional term in the equation of motion. This term describes the force on the shell at position x which arises from all the mass inside a sphere of radius x. The gravitational constant G can be chosen by the user, because in this problem we have to specify the unit for the mass (or the density) which we did not need to specify in the other applet.

Furthermore, we have to specify how the borders of the computing region should be treated: we assume that all the gas that passes the inner (left) boundary falling towards the centre is kept there and adds to the mass of the 'core' of the cloud. The outer border is open, so that gas may stream out, but since we assume that there is no gas outside, there is nothing coming in.

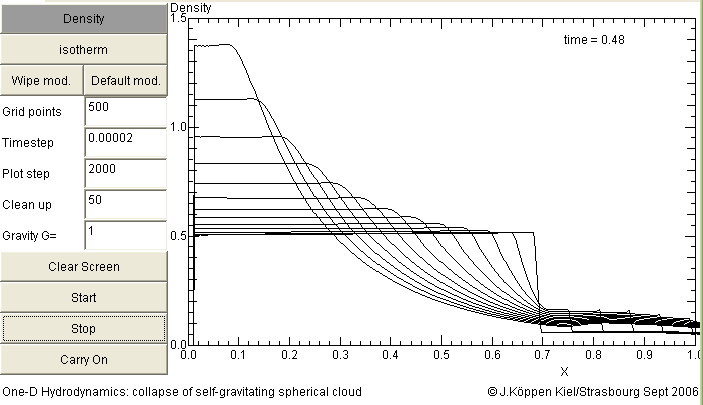
A standard case is the isothermal collapse: The evolution of the density profile shows that all the mass flows toward the centre, and that an initially flat profile remains flat. Only at the later time step, when most of the mass is in the central region, there will be some deviations. The outer boundary of the cloud expands with a shock into the low density gas around the cloud.

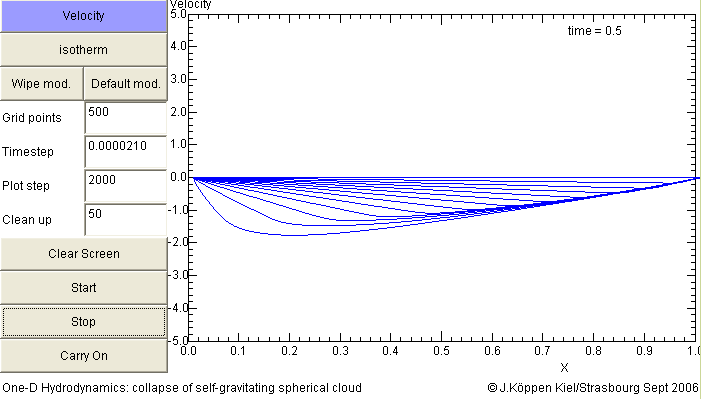
The velocity profile of isothermal collapse has a characteristic feature: the (negative) velocity increases linearly with radius and its profile becomes steeper with time, also linearly. The simulation shown here assumed an initially constant density:

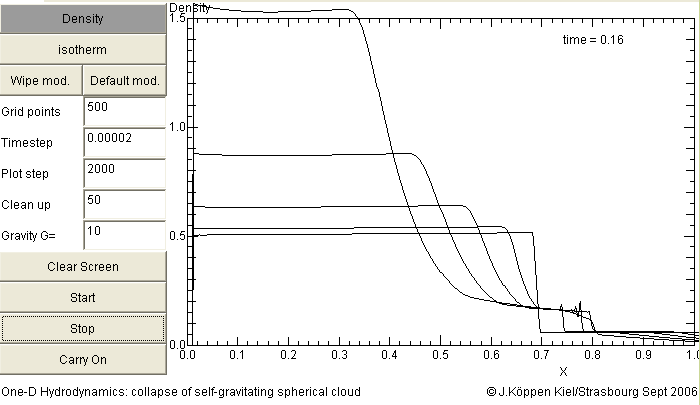
All the above models were done with G = 1. If we use a larger value for the gravitational constant, which is equivalent of having a higher density, we see that the collapse is faster ... This shows that the characteristic time (the free-fall time) decreases with density: T_freefall = (G * density)^(-1/2)

But if we use a smaller value, hence a smaller density, the collapse is less significant and the cloud dissolves into the surrounding near-vacuum, driven by the thermal pressure:

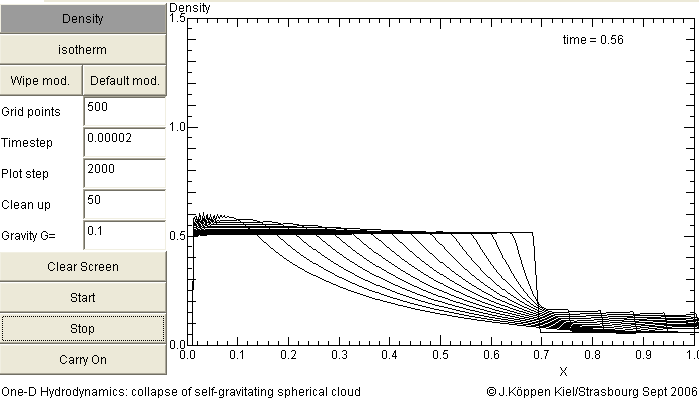
Also some numerical instabilities develop near the inner boundary. This is because the time step was chosen too large ...