Space Mirrors to Heat the Waters of an Atoll |
| Joachim Köppen Kiel/Strasbourg/Illkirch September 2006 |
Contents
The SpaceMirrors Applet and its early version compute how much flux from the Sun can be reflected onto a spot on Earth, as a function of time of the day, the height of the mirror's orbit, and the size and number of the mirrors. For simplicity, we assume that the orbits are circular and of zero inclination. Thus, the receiving site is somewhere on the Equator. If one had considered inclined orbits, one could have done the computations for other sites, say in Europe or in Siberia, but the computations would be a bit more complicated, the number of free parameters would have been larger, but one would not learn anything substantially different about the efficiency and the configuration of such a conceivable system. What we consider here, constitutes essentially the easiest and the most efficient case.
We also assume that the mirrors are always oriented in such a way that the sunlight is directed to the single site. This means that each mirror has to make less than one full turn during one orbit. The mirrors are assumed to work on both sides equally well, and that they are perfectly reflecting mirrors. If you want to influde any loss of sunlight, you may do so in multiplying the results with some efficiency factor. If several mirrors are employed, they are distributed evenly in the same orbit. We also neglect the effects of the Earth's atmosphere, notably the attentuation and the refraction of the incoming rays both of which would be largest when the mirrors are very close to the horizon. Of course, clouds and fog and any meteorological effects are neglected, which would only make the system less efficient.
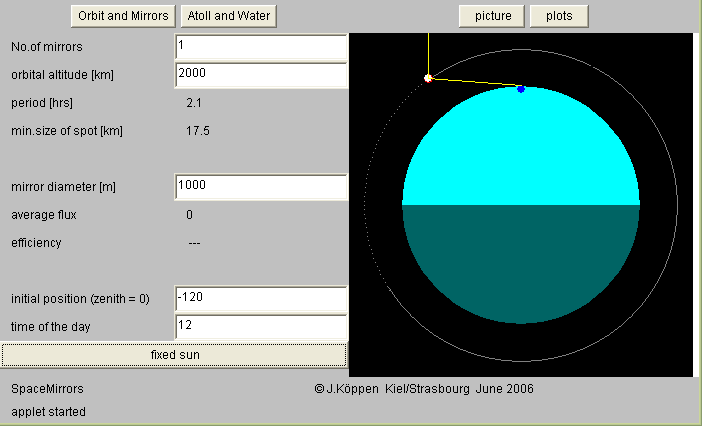
When the applet appears, one should best click on the picture Button and a schematic drawing of a single mirror in its orbit around the Earth appears (sometimes the figure might look odd or incomplete; then simply press the button a second time!):

The atoll is marked by the small blue dot on the top part of the Earth. The default start time of the day for this visualization is local noon, but you may see it at a different time by entering the value in the textfield and hitting the enter or return key. The Earth is shown with its daylit and nighttime sides. The (default) initial position of the mirror is at -120 degrees in latitude from the atoll. Again, one may change this value. The Button fixed sun indicates that for the display we shall pretend that the sun does not move in the sky as time goes by. The mirror is marked in yellow when it is in the sunshine, and white when it is also able to pass sunlight to the atoll.
The left hand panel allows us to set the No.of mirrors and the orbital altitude, and tells us the resulting period. Since the Sun extends an angle of about 0.5 degrees in the sky, the image of its reflection will also be finite. It depends on the distance to the satellite. min.size of spot is the value when the mirror is right overhead of the atoll. With an orbital height of 2000 km the spot is at least 17 km in diameter. Since the reflected solar radiation is spread out over this spot, the applet computes it from the current distances. The mirror diameter can be entered.
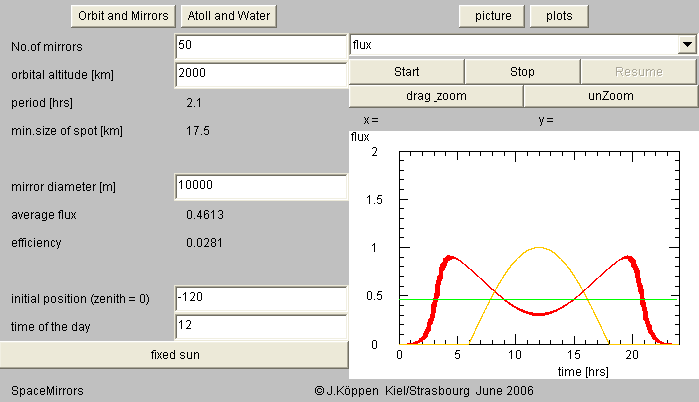
Clicking on the button plots allows to inspect the results of the simulation. The most interesting one is probably the flux of the light received at the site from the mirrors. It is given in units of the flux of the sun when it shines perpendicularly down on the site. To display the results click Start. For slow machines, or a large of mirrors it may be helpful to interrupt the simulation by Stop to be able to change parameters and restart with a better set. The flux (or any other quantity) is shown as a function of the time of the day, from local midnight to midnight:
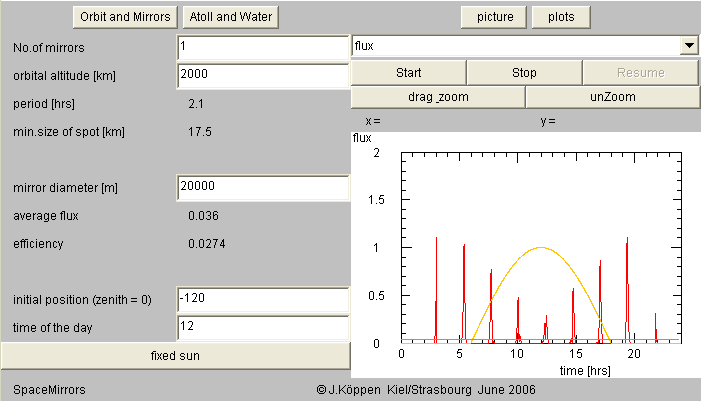
In the above simulation, we had taken a rather large mirror diameter to be able to see anything interesting ... The orange curve which peaks at noon is the solar flux received directly. It is less in the mornings and the evenings because the solar rays hit the surface of the atoll at an inclined angle. The red curve with its spikes is the flux received from the mirror. Each peak corresponds to an averhead passage of the mirror. As can be seen, with a orbital period of 2.1 hours the mirror makes 9 passages when it is sunlit.
On the left hand panel, the average flux is now given (and shown as the green horizontal line in the plot), in the same solar units. This is the average over an entire 24 hours. If you display flux from sun which shows the time variation as a red curve and the average as an orange horizontal line, you learn that a full day of direct sunshine gives an average flux of about 0.33. We also are informed about the efficiency which is defined as the average flux compared with the total flux that would be captured by the mirror if it were always oriented looking straight at the Sun. This value is just given for illustrative purposes. Due to the changing orientations, the values can never reach large values!
One notes that the reflected flux at noon is less than in the morning and evening passes: This is a geometrical effect which unfortinately cannot be avoided. When the mirror passes over the atoll while the Sun is also overhead, it cannot reflect any light to the atoll! Reflections are much better during morning or evening when the mirror - as seen from the site - is opposite of the Sun, so it can present its full face to the Sun and so receive and reflect the rays at normal incidence.
Since this single mirror - despite its size of 20 km - supplies only 4 percent of what the site receives directly from the sun, let us explore what happens if we put 5 mirrors into orbit?
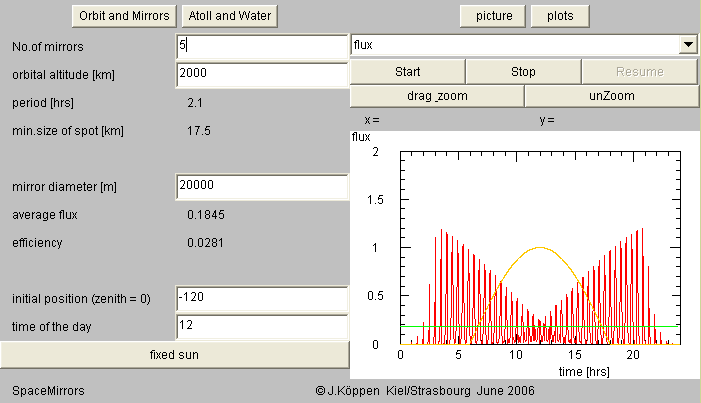
There are now many more passes which raise the reflected average flux to 18 percent. The peaks follow each other in rapid succession. If one clicks drag zoom, then drags the mouse over that part of the plot which one wants to zoom in, and then click Start again, one may see the fine details of the passes. To bring back the full view, click on unZoom, and then Start again. We note that the passes during the morning and evening are the more efficient ones. The orbital configuration of the mirrors shows that while some mirrors are in the Earth shade, there is almost always one sunlit mirror above the local horizon.
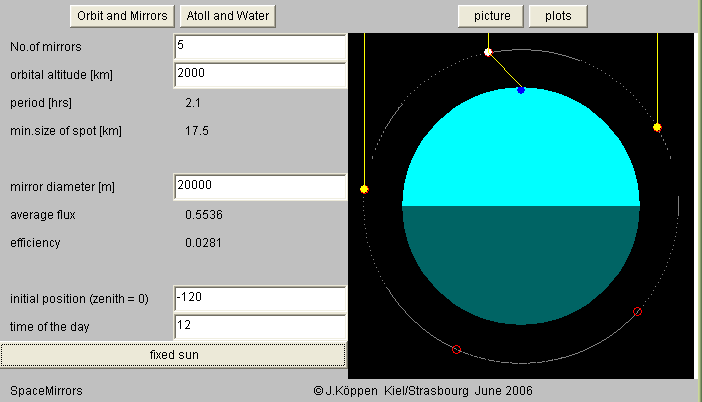
Please note that some of the variables which can be plotted - such as position angle of the mirror - apply specifically to a single mirror. When several mirrors are chosen, the quantity shown is that of only one of the mirrors. This was done to prevent the plots to become cluttered up with too many curves.
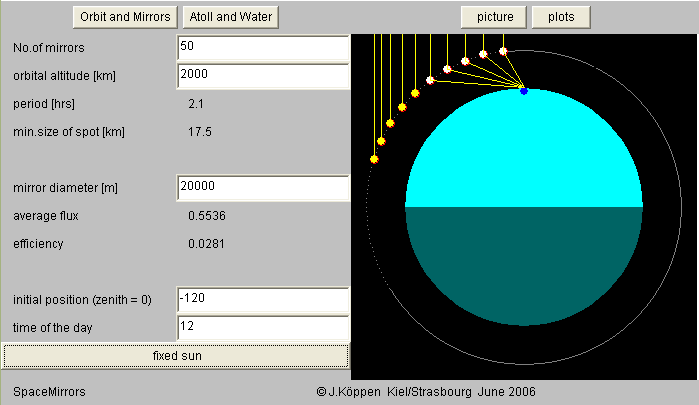
Things get much better, if we consider 50 mirrors: The flux curve never drops to zero during the day, as there are always several mirrors which reflect sunlight to the atoll. The peaks of the individual passes merge into a continuous curve, and the average flux now is a bit higher than the value from the direct sunlight alone, athough we had halfed the mirror diameter. Thus, one may expect better to be able to heat the water in the atoll.
In the orbital configuration we only show ten mirrors - otherwise the picture would be to cluttered to see anything. It is obvious that there are always several sunlit mirrors above the horizon.
To estimate the effect of this heating on the waters in the atoll, we compute in a simplified model the water temp. (sun+mirrors):
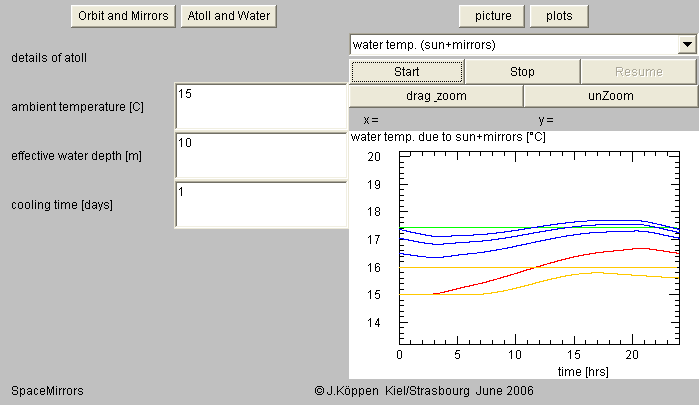
On the left hand panel (which opens via the Atoll and Water Button) one has to specify the ambient temperature, effective water depth which is the thickness of the water layer that is being heated, and the cooling time which is a rough way to account for the heat losses due to radiation and conduction. The results in the plot on the right show several things:
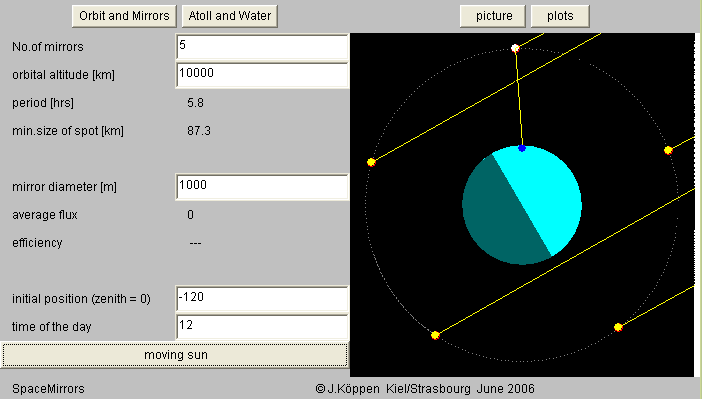
Finally, we may also show the orbital configuration how it changes during one day, since the Sun moves with respect to the atoll. Here are five mirrors, on a higher orbit, seen during the local afternoon. One mirror is in the zenit, one has just set, but another will soon rise:
| Top of the Page | Project's HomePage | Applet | Applet Index |