Model Population of Stars

J.Köppen Strasbourg/Illkirch/Kiel May 2001

-------- under modernisation -----------

Contents

About the Applet and what it does

The luminous matter in the Universe is organized in galaxies which consist of stars and interstellar gas. The stars have been born at various times in the past from the gas by cold molecular clouds becoming unstable against their own gravity. Nearly all the optical brightness of a galaxy comes from the present stellar population which thus may be a combination of young and old, hot and cool stars. From theoretical work, it is fairly well known how stars of the various masses change with time, so it is possible to model a population of stars, in order to find out how star formation occurred in the past. Because star formation is something we still cannot derive from basic physics. So one describes this process by assuming that stars are born following a certain distribution Function of their Initial Masses (the IMF, usually decreasing like a power law with increasing mass), and that the star formation rate (SFR) describes how much gaseous matter is converted per time unit into any kind of stars. The evolution of the new stars depends on the metallicity of the gas out of which they were formed.

The StarPop Applet allows to compute the theoretical and observable properties of single stars of any mass and age and various metallicities. It also permits to create synthetic populations of stars born with any arbitrary history star formation.

A Tour around the Applet

This is how your screen should look like after the applet has been loaded and started, and you have clicked Clear:

There is a white plotting area and some controls on the top:
Clear to >>>>
will clear the plotting area to show the diagram whose axes will be as indicated on the right:
X = Teff (log)
selects what is to be meant by the x-axis. Here, the effective temperature of the star(s) is chosen. The (log) indicates merely that the axis will be divided in logarithmic fashion, which is useful for the large range of temperatures that need to be shown
Y = lg(L)
ditto, for the y-axis. Here, the logarithm of the luminosity (in units of solar luminosity) is chosen
These controls are accessible in all the pages.

There are quite a few controls on the left hand side. At the top the principal buttons Setup, Star, Simulate, Select, Colour, and XY Histogram are placed. These are used for navigating in the applet. Right now we are in the Star menu, and beneath we find all its revelant controls:

Mass
here one enters the mass of the star (in solar masses)
Track
clicking this button will plot as a blck curve the evolutionary track of the star with above given mass until the age given below
Age [Gyr]
the age of the star, or the maximum age of a star on its track
Isochrone
clicking this button will plot as a red curve the position of stars of all masses, but of a given age
Star
clicking this marks with a black dot the position of the star with given mass and age ...
Teff
... for which the effective temperature will be shown ...
log(L)
... as well as its luminosity
drag & Zoom
click the button and drag (move while keep the button pressed) the mouse over any area of the plotting screen will select this rectangular area for the new view. Note that everything plotted before will be wiped, and you'll have to re-draw
unZoom
brings back the default view of the plot

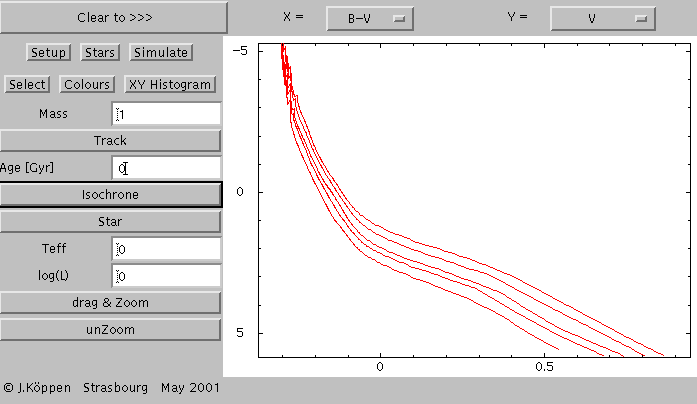
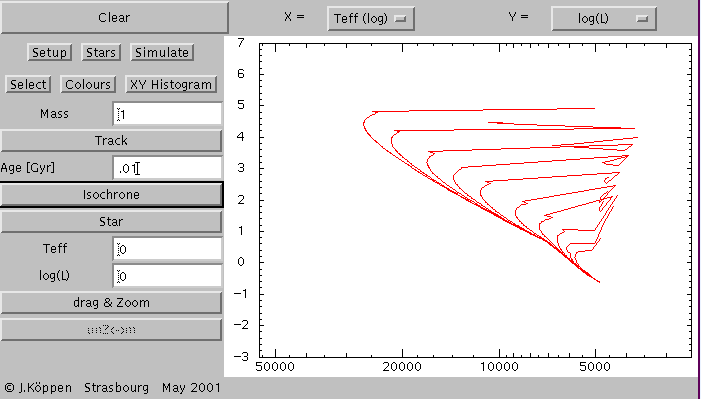Here we have plotted the isochrones for ages of 0.01, 0.02, 0.05, ..., 2, 5, and 10 Gyrs (from left to right).

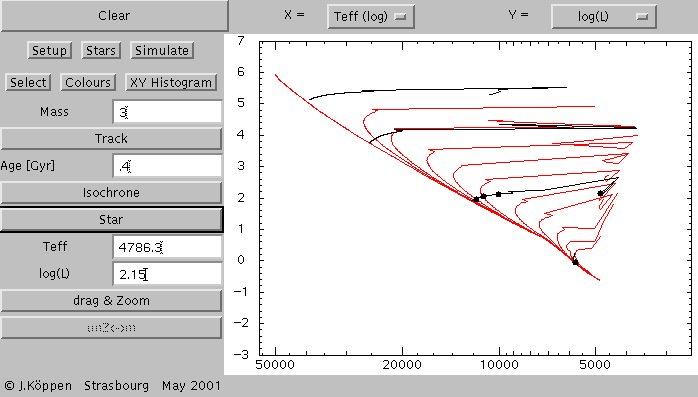And here we added the evolutionary tracks of stars with 1, 3, 10, and 30 solar masses (black curves), the zero-age isochrone (red curve), and the positions (black dots) of a 3 solar mass star at ages of 0.1, 0.2, 0.3, and 0.4 Gyrs. The effective temperature and luminosity of the last position is shown in the text fields. Also shown is the position of a 1 solar mass star at an age of 3 Gyrs.

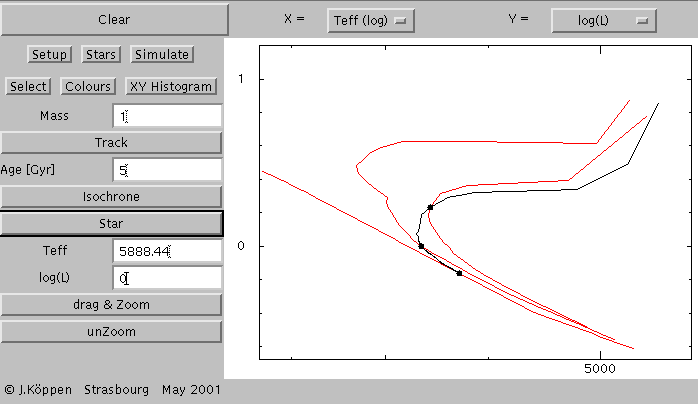Now the area near the present solar position is zoomed by using the Drag & Zoom button and dragging the mouse over a suitable area. One may zoom as deeply as one wishes, however the labels on the axis tick marks will eventually disappear, and one may also rather quickly notice the effects of linear interpolation in the evolutionary track data! The unZoom button will always bring back the overall view. All graphics will be erased, and we show the isochrones for 0, 5, and 10 Gyrs, the complete track of a 1 solar mass star (specifying 20 Gyrs age), and the positions of the sun at ages 0, 10, and 5 Gyrs, the latter's temperature and luminosity are given.

So far, we showed only the normal Hertzsprung-Russell diagram. The Choices at the top permit to select any two of the following stellar parameters as X- or Y-axis:

Teff (log)
effective temperature
log(L)
log of luminosity, in solar units
R* (log)
star's radius, in solar units
M* (log)
mass, in solar units
log(g)
log of the star's surface gravity, in cm/s^2
age [Gyr]
star's age, shown in linear scale
age (log)
age, but in logarithmic scale
U
brightness in the U-band (about 365 nm wavelength), in magnitudes
B
brightness in B-band (440 nm)
V
brightness in V-band (548 nm)
U-B
colour index = difference of U and B magnitudes
B-V
colour index
SFH
Star Formation History, the star formation rate as a function of age

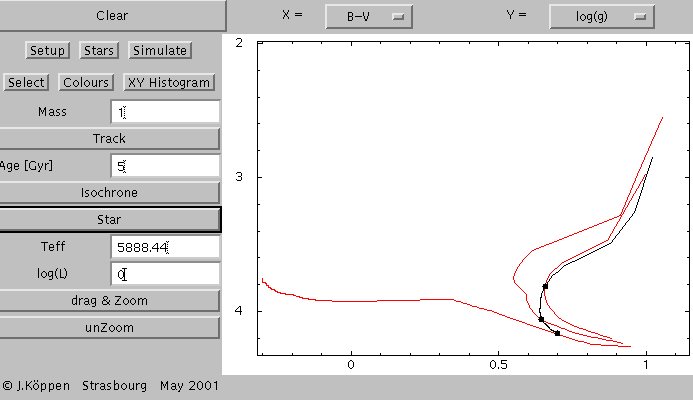This is the same set of curves as before, but in the diagram of B-V colour index against the surface gravity g, also zoomed to bring out the interesting parts.

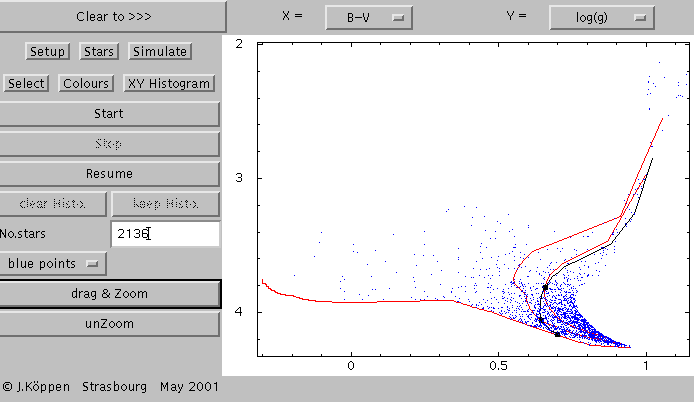From the last picture, we've switched over to the Simulate page. This has these controls:
Start
starts a Monte Carlo simulation to create stars with certain mass spectrum and certain star formation history
Stop
halts the simulation
Carry on
continues with the simulation.
Clear Histo.
clears any simple histogram we may have kept from earlier simulations
keep Histo.
keep the present histogram in memory, and superimpose it with any further results
No. stars
shows the number of stars simulated so far
blue points
allows to change the colour of the plotting points: red, blue, green, black are available
drag & Zoom
click the button and drag (move while keep the button pressed) the mouse over any area of the plotting screen will select this rectangular area for the new view. Note that everything plotted before will be wiped, and you'll have to re-draw
unZoom
brings back the default view of the plot

Let us now click the Start button, and after a while the Stop: We have created a stellar population of about 2000 stars, whose positions are indicated as blue dots. We'll return to this later, but what is behind all this?

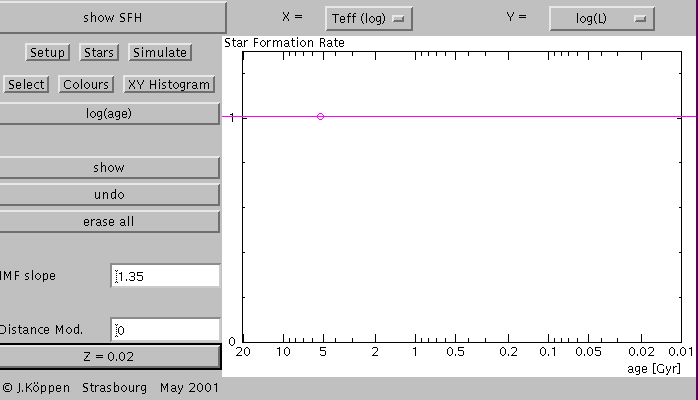This is shown by the Setup page. It displays the star formation history only, and has these controls:
log(age)
switches between linear and logarithmic scale for the age axis
show
just refreshes the plot
undo
removes the data point entered last
erase all
removes all data points
IMF slope
shows the exponent of the power-law function assumed for the distribution of initial masses of stars in a population. 1.35 means the Salpeter law, i.e. the mass contained in stars with masses between m and m+dm decreases like the 1.35rd power of m
Distance Mod.
the distance modulus for the population.
Z = 0.02
metallicity assumed for the stellar evolutionary tracks and the photometric colours. Z= 0.02 means that 2 percent of the mass of a piece of the star is in the form of 'metals', elements heavier than helium. This is the solar value. Z = 0.001, 0.004, 0.008, 0.02, and 0.04 are available

From this we see that in the present simulation the star formation rate is taken as being constant for all ages (from 10 million to 20 Gyrs), that solar metallicity (Z=0.02) had been assumed for the evolutionary tracks. And that the IMF slope was 1.35, i.e. we had assumed a Salpeter initital mass function.

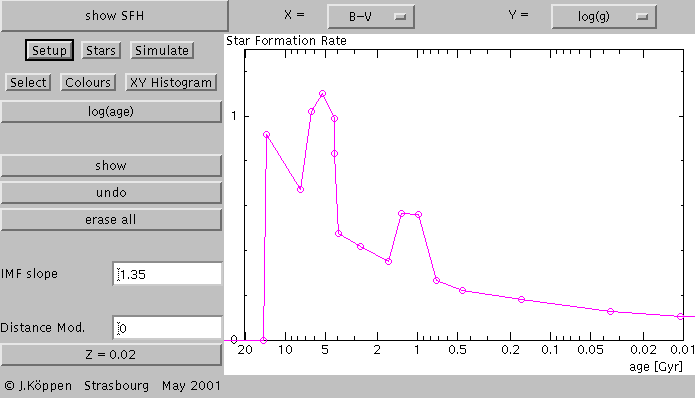Let us first play with the star formation history: Just click with the mouse on the plotting screen. A small mauve circle will mark the datum. One can grab the circle and move it about. If you are in what is the current SFH, click either Clear SFH, show, or merely move one of the data points a bit. Let us here assume that on some background rate which increases with age - because in the past there was still more gas available to make stars than today, and of course no star formation before the Big Bang (about 15 Gyrs ago) - we put one star burst, about 1 Gyr ago:

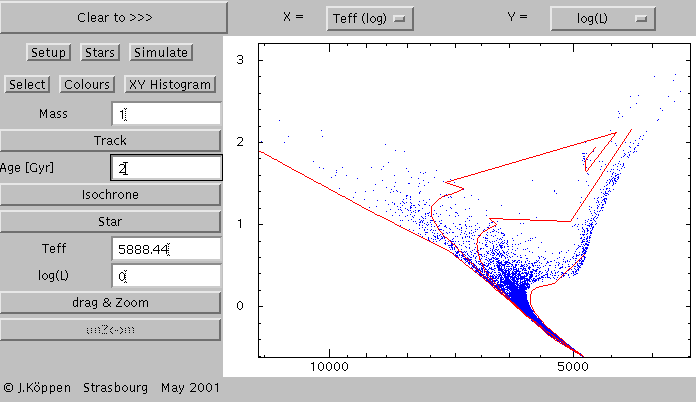This is what we got from the simulation: We have overlaid the simulated Hertzsprung-Russell Diagram with the isochrones of 0, 1, 2, and 13 Gyrs. We can see that just to the left of the 1 Gyr isochrone the stars are more numerous. But also that the diagram is still dominated by the underground star formation.

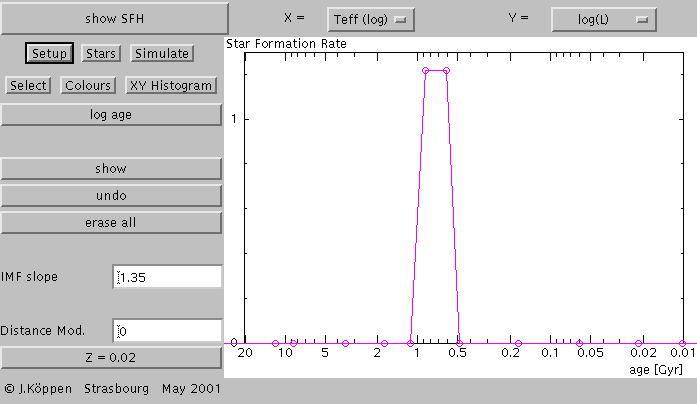To isolate the effects of the different populations, we can first regard the burst with the above star formation history...

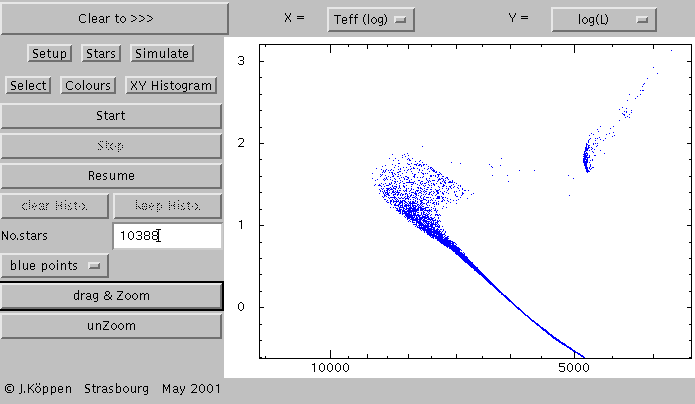... which makes this zoomed HRD. Now - do NOT click the Clear button! - let us go back to the Setup page

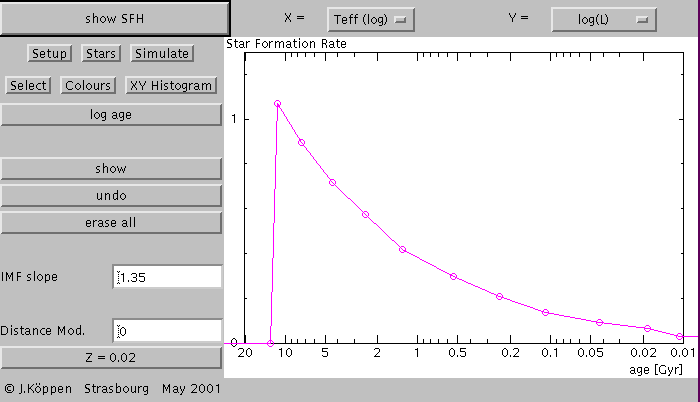and compose the underlying star formation

Then we go back to Simulate page - again: do not press Clear! Here we first change the colour of the points from blue to say: red, and then we click Start button. This will add the second population to what was on the screen. If we run this for a while, say up to twice as many stars we had in the burst population, we get this

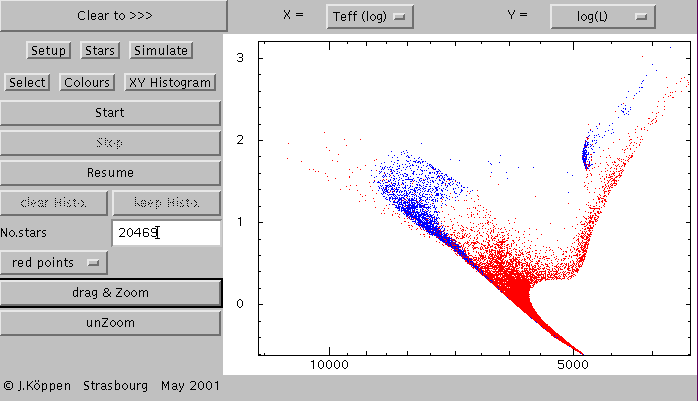where we can easily identify that the burst population will dominate among the hot stars - only few are produced in the background population, it will also contribute to the red giant stars, but the older background population dominates both among the red giants and the fainter stars close to the main sequence.

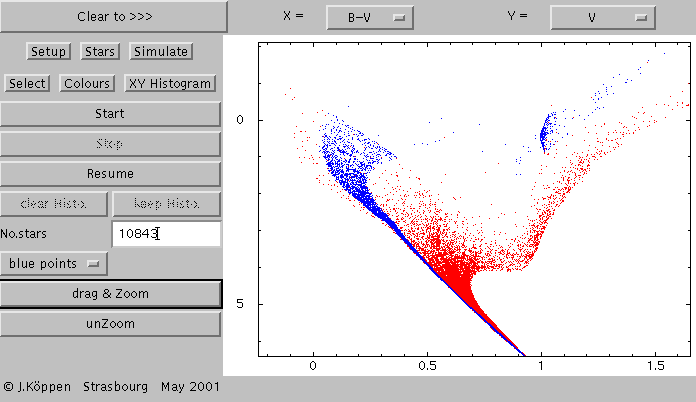What we observe directly is the colour-magnitude diagram, e.g. B-V against V, done for the same populations which indicates that one could discriminate between the populations in a histogram of the B-V colour indices.

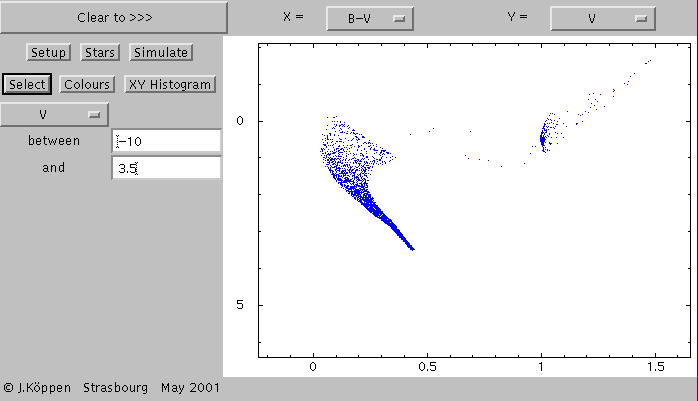But before we make the histogram, let us select only stars which are brighter than say 6.5 magnitudes in V. This is done on the Select page, Its controls are:
no selection
this Choice allows to choose one parameter for whose values the simulated stars will be selected
.......
the text fields specify the lower and upper limit of the acceptable values. Note that we mean numerically upper and lower value, i.e. when stars brighter than 5th magnitude should be accepted, one specifies -100 and 5!
and the above plot shows the result of the simulation of the burst population.

You may have noticed that the Choice for the Y-axis also has an entry Histogram. When chosen, a histogram of the parameter selected for the X-axis will be done:

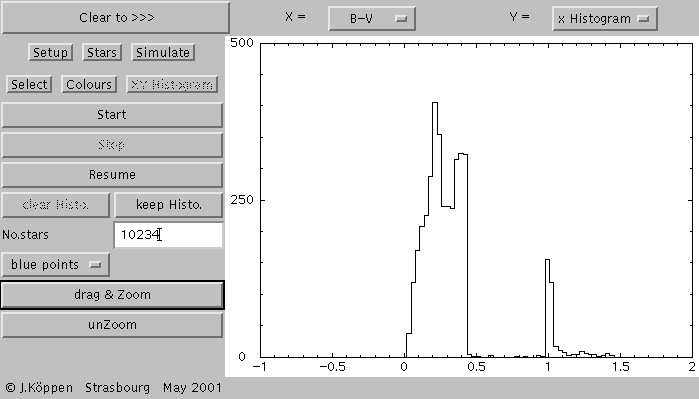This is the histogram of B-V colour from 10000 stars of the burst population. As the histogram builds up, the picture is automatically rescaled whenever the peak values become sufficiently large. By clicking the keep Histo. button we save this curve.

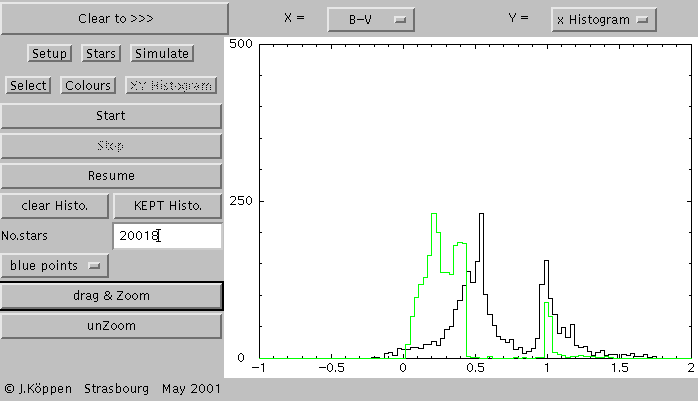And this is what one gets for 20000 stars from the background population, this is shown by the black curve, while the green curve shows the saved histogram of the burst population, scaled to the same maximum value.

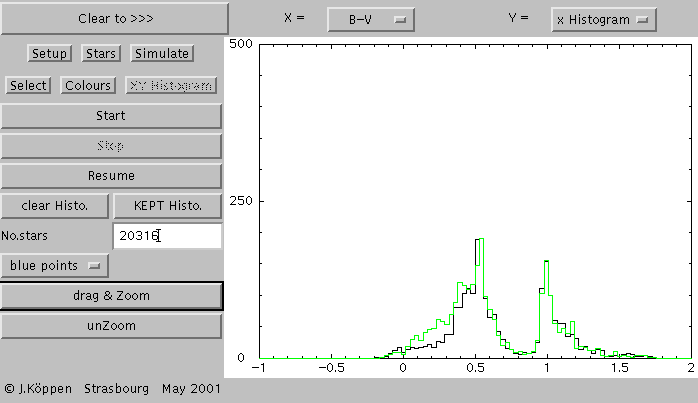Here we compare the 30000 stars of the composite star formation history (green histogram; oh yes, one had to enter this in the Setup page) and 20000 stars of the background only (black). The two histograms are very similar, but the composite population has more bluer stars, with colours B-V between 0 and 0.5. One has to look carefully, if one has only colours.

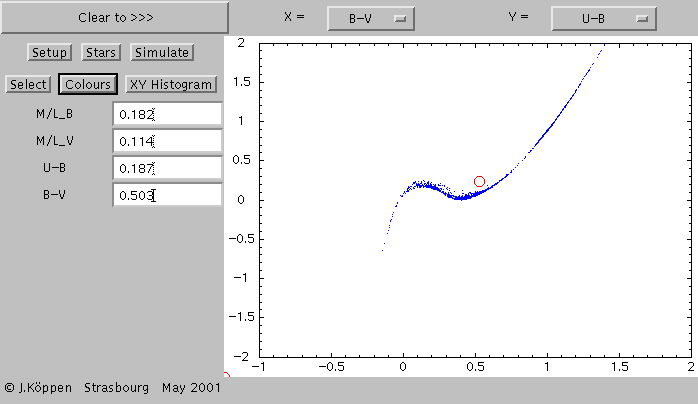
One can also get the integrated colours of the whole population. While a simulation is going on, one may click the button for the Colour page and every 50 stars, the colour indices U-B and B-V as well as the ratios of mass-to-luminosity in the B and V bands are displayed. So one can watch until the numbers are sufficiently stable, and stop the simulation. When the two-colour diagram X=B-V and Y=U-B are selected, a red circle appears to show the integrated colours:

Finally, we can show all diagrams also as a colour-coded plot of the number density of points in each area of the diagram. This is the XY-Histogram

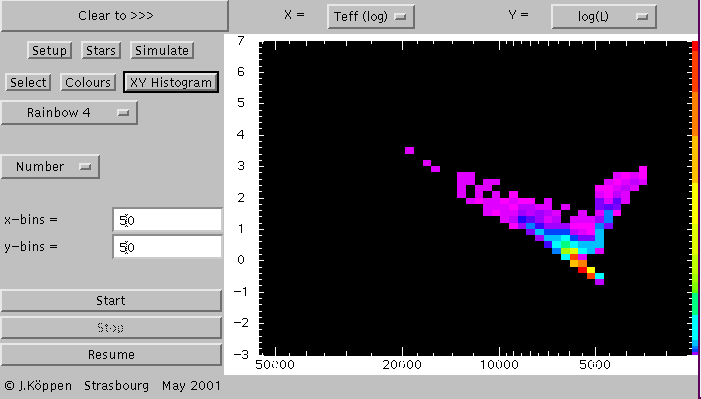Here is the plot for the composite population, now with the selection in V magnitude again switched off.

The controls are:

Rainbow 4
selects the type of colour coding, such as Raimbow, White-on-Black, Black-on-White, Warm. The number indicates with what power law the coding is distorted, as to emphasize the large values (-4, -2) or the small values (4, 2). In any case, the current color bar is displayed as a narrow strip to the right of the plot area, showing the coding between 0 (bottom) and 100 percent (top).
Number
selects what is shown by the colours: the number density, or weighted with the mass, luminosity, U-, V-, B-luminosities, or the B-V or U-B colour indices.
x-bins, y-bins
give the numbers of bins for the x- and y-coordinates. More bins give finer resolution, but also require more time to paint the plot. There is no limit to the number of bins one may employ; the main limitations are the available space on your machine and your patience to seen all points to redrawn.
Start
starts the simulation ...
Stop
... halts it ...
Resume
... continues with the current simulation

Weighting with U-luminosity shows the Hertzsprung-Russell Diagram for our population, here in a gray-scale representation.

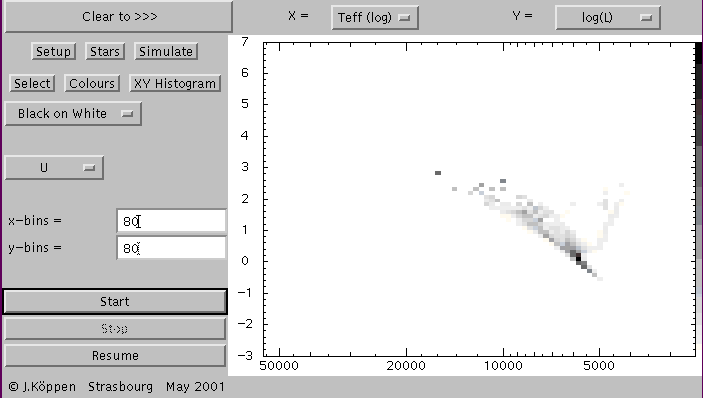The hot main sequence stars contribute much because of their luminosity and temperature, but the cooler main sequence stars also contribute because of their large number. Red giants are not strong contributors to the U-luminosity.

As the histogram builds up, the picture is automatically rescaled whenever the peak values become sufficiently large.

The XY-Histograms can also be done for a zoomed view: zooming is done from the Star or Simulate pages.

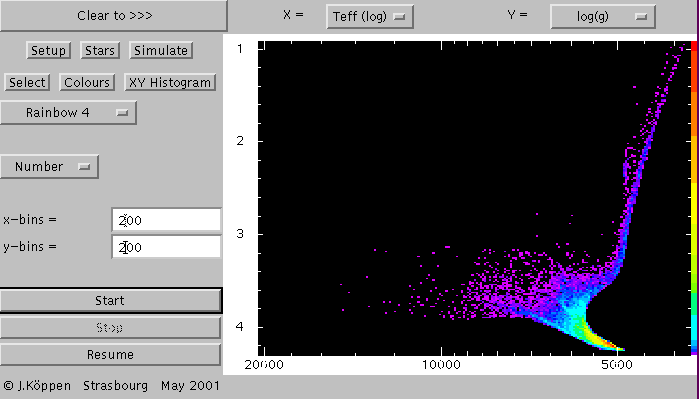
Some Experiments

Here is a view of a portion of the Hertzsprung-Russell diagram in the form of effective temperature and surface gravity: the blue dots are stars of very low metallicity (Z = 0.001), the red ones have solar metallicity.

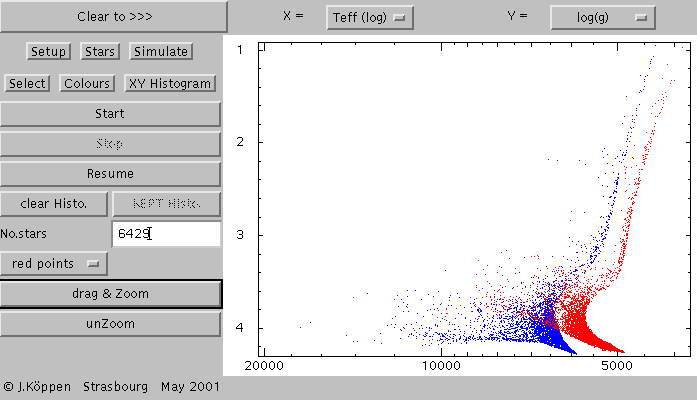
This plot shows the zero-age isochrones of all metallicities 0.001, 0.004, 0.008, 0.02, and 0.04 (from left to right). The curves are not smooth curves in the upper left hand corner. This is because of our rather simplified interpolation of the colour corrections.

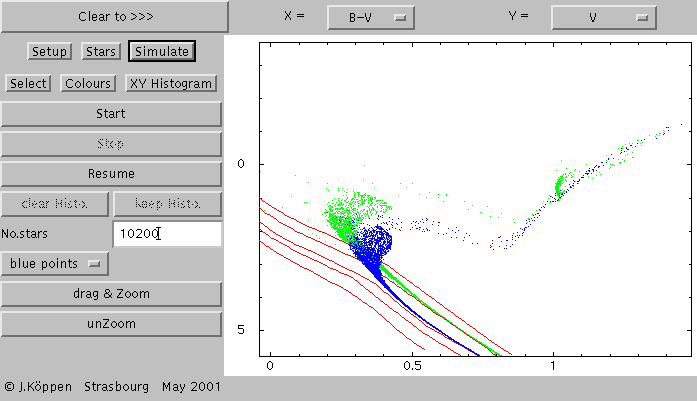
The zero-age isochrones (in red) are overlaid with two stellar populations: In green, a solar metallicity, 1 Gyr old population, in blue one with roughly half metallicity (Z = 0.008) but twice as old. The integrated colours are quite similar, showing the age-metallicity degeneracy.

Details:

The applet uses the theoretical evolutionary tracks computed by the Geneva group. The photometric colours are computed using tables calculated with the Kurucz' grid of theoretical stellar spectra.

The initial mass function (IMF) is assumed to be is a power law in the range of stellar masses between 0.8 to 120 solar masses. The value of the exponent of 1.35 refers to Salpeter's IMF.

| Top of the Page | Controls | Applet | Applet Index |