Mathematical functions. More...

Functions/Subroutines
elemental real function, public	asinh (x)
	inverse hyperbolic sine function More...

elemental real function, public	acosh (x)
	inverse hyperbolic cosine function More...

elemental real function, public	atanh (x)
	inverse hyperbolic tangens function More...

elemental real function, public	heaviside (x, a)
	step function More...

elemental real function, public	barrier (x, a, b)
	barrier function More...

elemental subroutine, public	normalrand (u1, u2, x, y)
	Box-Muller alg. for gaussian distributed random variables input are uniform distributed random variables [0,1) More...

elemental subroutine, public	ellipticintegrals (k, Kell, Eell)
	compute the complete elliptic integrals of first and second kind using the AGM method (arithmetic-geometric-mean); More...

elemental real function, public	ellipticintegral_k (k)
	compute the complete elliptic integral of the first kind using the AGM method (arithmetic-geometric-mean) More...

elemental real function, public	ellipticintegral_e (k)
	compute the complete elliptic integral of the second kind using the AGM method (arithmetic-geometric-mean) More...

elemental real function	rf (x, y, z)
	Computes Carlson's elliptic integral of the first kind R_F(x,y,z), y,y,z > 0. One can be zero. TINY must be at least 5x the machine underflow limit, BIG at most one fifth of the machine overflow limit. similar to Numerical recipes 2nd edition. More...

elemental real function	rd (x, y, z)
	Computes Carlson's elliptic integral of the second kind R_D(x,y,z), y,y > 0. One can be zero. z > 0. TINY must be at least twice -2/3 power of the machine underflow limit, BIG at most 0.1 x ERRTOL times the -2/3 power of the machine overflow limit. similar to Numerical recipes 2nd edition. More...

elemental real function, public	incompleteellipticintegral_f (phi, ak)

elemental real function, public	incompleteellipticintegral_e (phi, ak)
	Legendre elliptic integral of the second kind E(phi,k), evaluated using Carlson's function R_D and R_F. The argument ranges are 0 <= phi <= pi/2, 0 <= k*sin(phi) <= 1 similar to Numerical recipes 2nd edition. More...

pure subroutine, public	legendrepolynomials (l, x, P)

elemental real function	legendrepolynomial_one (l, x, Plminus1, Plminus2)

elemental real function	legendrepolynomial_all (l, x)

elemental real function, public	legendrefunction_qminhalf (x)
	Computation of the order 0 and -1/2 degree Legendre function of the second kind Q_{-1/2} using the AGM method (arithmetic-geometric-mean) More...

elemental real function, public	bessel_i0 (x)
	Compute the modified Bessel function of the first kind as polynomial expansion, which has been proposed by Numerical Recipes in fortran, Second Edition on page 229ff. Nontheless the implementation is different and only the idea is used. More...

elemental real function, public	bessel_i1 (x)
	Compute the modified Bessel function of the first kind as polynomial expansion, which has been proposed by Numerical Recipes in fortran, Second Edition on page 229ff. Nontheless the implementation is different and only the idea is used. More...

elemental real function, public	bessel_k0 (x)
	Compute the modified Bessel function of the second kind as polynomial expansion, which has been proposed by Numerical Recipes in fortran, Second Edition on page 229ff. Nontheless the implementation is different and only the idea is used. More...

elemental real function, public	bessel_k0e (x)
	Compute the exponential scaled modified Bessel function of the second kind e.g. K0e = EXP(x) * K0(x) as polynomial expansion, using coefficients from Abramowitz p.379 (http://people.math.sfu.ca/~cbm/aands/page_379.htm) for x >= 2, and exp(x)*K0(x) directly for 0<x<2. More...

elemental real function, public	bessel_k1 (x)
	Compute the modified Bessel function of the second kind as polynomial expansion, which has been proposed by Numerical Recipes in fortran, Second Edition on page 229ff. Nontheless the implementation is different and only the idea is used. More...

elemental real function, public	ei (x)
	Computes the exponential integral Ei(x) for x != 0 Ei(x) := int_-oo^x exp(t)/t dt Implementation similar to: http://www.mymathlib.com/functions/exponential_integrals.html. More...

elemental real function	continued_fraction_ei (x)

elemental real function	power_series_ei (x)

elemental real function	argument_addition_series_ei (x)

elemental real function, public	errorfunc (x)
	returns the error function of argument x calculation of error fuction and complementary errorfunction are based on M. Abramowitz and I. A. Stegun: Handbook of Mathematical Functions, Applied Mathematics Series. National Bureau of Standards, Vol. 55, 1964 online resource: http://people.math.sfu.ca/~cbm/aands/ and "Rational Chebyshev approximations for the error function" by W. J. Cody, Math. Comp., 1969, PP. 631-638. Coefficients for the Polynoms are taken from the library routine http://www.netlib.org/specfun/erf written by W. J. Cody More...

elemental real function, public	comperrorfunc (x)

elemental real function	codyerfapprox (x)

elemental real function	codycerf1approx (x)
	Cody approximation for complementary error function for 0.46875 < \|x\| < 4. More...

elemental real function	codycerf2approx (x)
	Cody approximation for complementary error function for \|x\| > 4. More...

elemental real function, public	inverf (x)
	Inverse of the error function Argument of this function has to be in ]-1,1[, returns huge(1.0) for values x with abs(x)>=1 without an error !!!! uses and idea of P.J. Acklam http://home.online.no/~pjacklam/notes/invnorm/ to calculate the inverse using the Halley root finding algorithm Halley is preferable to Newton- Raphson as the second derivative can be computed easily f''(y) = -2y*f'(y) for f(y)=erf(y) More...

elemental real function, public	gamma (x)
	Compute the Gamma function for arguments != 0,-1,-2,.. More...

elemental real function, public	lngamma (x)
	computes the logarithm of the gammafunction with Lanczos approximation found in Numerical Recipes for C++ p. 257 (different implementation) coefficiants from Paul Godfrey for g=607/128 and N=15 http://my.fit.edu/~gabdo/gamma.txt Gamma(x+1)=x! More...

Variables
real, parameter	pi = 3.14159265358979323846

real, parameter	sqrt_two = 1.41421356237309504880

real, parameter	eps_agm = EPSILON(EPS_AGM)

integer, parameter	max_agm_iterations = 20

integer	iii

integer, parameter	max_pl_coeff = 20

real, dimension(max_pl_coeff), parameter	pl_coeff = (/ (iii/(iii+1.0), iii=1,MAX_PL_COEFF) /)

Detailed Description

Mathematical functions.

Author: Tobias Illenseer; Manuel Jung; Björn Sperling

This module implements several mathematical functions, including

inverse hyperbolic sine, cosine and tangens
complete elliptic integrals of first and second kind
error and inverse error function
some Bessel functions of the first and second kind
exponential integral function Ei(x)
Gamma function

Function/Subroutine Documentation

◆ acosh()

elemental real function, public functions::acosh ( real, intent(in) x )

inverse hyperbolic cosine function

Definition at line 109 of file functions.f90.

Here is the caller graph for this function:

◆ argument_addition_series_ei()

elemental real function functions::argument_addition_series_ei ( real, intent(in) x )

private

Definition at line 850 of file functions.f90.

Here is the caller graph for this function:

◆ asinh()

elemental real function, public functions::asinh ( real, intent(in) x )

inverse hyperbolic sine function

Definition at line 99 of file functions.f90.

Here is the caller graph for this function:

◆ atanh()

elemental real function, public functions::atanh ( real, intent(in) x )

inverse hyperbolic tangens function

Definition at line 119 of file functions.f90.

◆ barrier()

elemental real function, public functions::barrier	(	real, intent(in)	x,
		real, intent(in)	a,
		real, intent(in)	b
	)

barrier function

Definition at line 142 of file functions.f90.

Here is the call graph for this function:

◆ bessel_i0()

elemental real function, public functions::bessel_i0 ( real, intent(in) x )

Compute the modified Bessel function of the first kind as polynomial expansion, which has been proposed by Numerical Recipes in fortran, Second Edition on page 229ff. Nontheless the implementation is different and only the idea is used.

Definition at line 576 of file functions.f90.

Here is the caller graph for this function:

◆ bessel_i1()

elemental real function, public functions::bessel_i1 ( real, intent(in) x )

Compute the modified Bessel function of the first kind as polynomial expansion, which has been proposed by Numerical Recipes in fortran, Second Edition on page 229ff. Nontheless the implementation is different and only the idea is used.

Definition at line 614 of file functions.f90.

Here is the caller graph for this function:

◆ bessel_k0()

elemental real function, public functions::bessel_k0 ( real, intent(in) x )

Compute the modified Bessel function of the second kind as polynomial expansion, which has been proposed by Numerical Recipes in fortran, Second Edition on page 229ff. Nontheless the implementation is different and only the idea is used.

Definition at line 656 of file functions.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

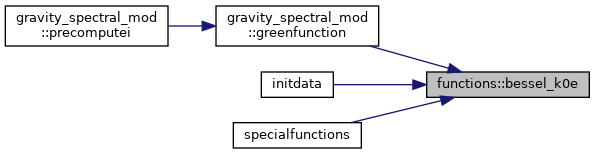
◆ bessel_k0e()

elemental real function, public functions::bessel_k0e ( real, intent(in) x )

Compute the exponential scaled modified Bessel function of the second kind e.g. K0e = EXP(x) * K0(x) as polynomial expansion, using coefficients from Abramowitz p.379 (http://people.math.sfu.ca/~cbm/aands/page_379.htm) for x >= 2, and exp(x)*K0(x) directly for 0<x<2.

Definition at line 691 of file functions.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

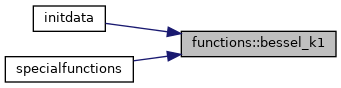
◆ bessel_k1()

elemental real function, public functions::bessel_k1 ( real, intent(in) x )

Compute the modified Bessel function of the second kind as polynomial expansion, which has been proposed by Numerical Recipes in fortran, Second Edition on page 229ff. Nontheless the implementation is different and only the idea is used.

Definition at line 720 of file functions.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ codycerf1approx()

elemental real function functions::codycerf1approx ( real, intent(in) x )

private

Cody approximation for complementary error function for 0.46875 < |x| < 4.

Definition at line 1014 of file functions.f90.

Here is the caller graph for this function:

◆ codycerf2approx()

elemental real function functions::codycerf2approx ( real, intent(in) x )

private

Cody approximation for complementary error function for |x| > 4.

Definition at line 1051 of file functions.f90.

Here is the caller graph for this function:

◆ codyerfapprox()

elemental real function functions::codyerfapprox ( real, intent(in) x )

private

Definition at line 984 of file functions.f90.

Here is the caller graph for this function:

◆ comperrorfunc()

elemental real function, public functions::comperrorfunc ( real, intent(in) x )

Definition at line 952 of file functions.f90.

Here is the call graph for this function:

◆ continued_fraction_ei()

elemental real function functions::continued_fraction_ei ( real, intent(in) x )

private

Definition at line 779 of file functions.f90.

Here is the caller graph for this function:

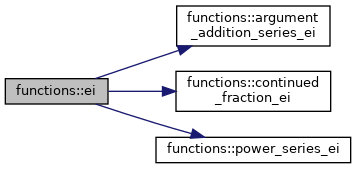
◆ ei()

elemental real function, public functions::ei ( real, intent(in) x )

Computes the exponential integral Ei(x) for x != 0 Ei(x) := int_-oo^x exp(t)/t dt Implementation similar to: http://www.mymathlib.com/functions/exponential_integrals.html.

Definition at line 757 of file functions.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ ellipticintegral_e()

elemental real function, public functions::ellipticintegral_e ( real, intent(in) k )

compute the complete elliptic integral of the second kind using the AGM method (arithmetic-geometric-mean)

returns NaN on error, i.e. for |k| > 1

Definition at line 274 of file functions.f90.

Here is the call graph for this function:

◆ ellipticintegral_k()

elemental real function, public functions::ellipticintegral_k ( real, intent(in) k )

compute the complete elliptic integral of the first kind using the AGM method (arithmetic-geometric-mean)

returns NaN on error, i.e. for |k| > 1 compute the complete elliptic integral of the first kind using the AGM method (arithmetic-geometric-mean)

returns NaN on error, i.e. for |k| > 1

Definition at line 237 of file functions.f90.

◆ ellipticintegrals()

elemental subroutine, public functions::ellipticintegrals	(	real, intent(in)	k,
		real, intent(out)	Kell,
		real, intent(out)	Eell
	)

compute the complete elliptic integrals of first and second kind using the AGM method (arithmetic-geometric-mean);

Function definitions and algorithm are given in [1] M. Abramowitz and I. A. Stegun: Handbook of Mathematical Functions, Applied Mathematics Series. National Bureau of Standards, Vol. 55, 1964 online resource: http://people.math.sfu.ca/~cbm/aands/

check the value of K(k): (a) K((SQRT(6)-SQRT(2))/4) = 2**(-7/3) * 3**(1/4) * Gamma(1/3)**3 / PI (b) K(1/SQRT(2)) = SQRT(PI)/4 * Gamma(1/4)**2 (c) K((SQRT(6)+SQRT(2))/4) = 2**(-7/3) * 3**(3/4) * Gamma(1/3)**3 / PI

check value of E(k): (a) E((SQRT(6)-SQRT(2))/4) = SQRT(PI)*3**(-1/4) * ( 2**(1/3) / SQRT(3) * (SQRT(PI)/Gamma(1/3))**3

0.125*(SQRT(3)+1) / (2**(1/3)) * (Gamma(1/3)/SQRT(PI))**3) (b) E(1/SQRT(2)) = SQRT(PI)*(PI/(Gamma(1/4)**2)+0.125*(Gamma(1/4)**2)/PI) (a) E((SQRR(6)+SQRT(2))/4) = SQRT(PI)*3**(1/4) * ( 2**(1/3) / SQRT(3) * (SQRT(PI)/Gamma(1/3))**3
0.125*(SQRT(3)-1) / (2**(1/3)) * (Gamma(1/3)/SQRT(PI))**3)

with Gamma(1/3) = 2.6789385347 ... and Gamma(1/4) = 3.6256099082 ...

returns NaN on error, i.e. for |k| > 1

Definition at line 191 of file functions.f90.

Here is the caller graph for this function:

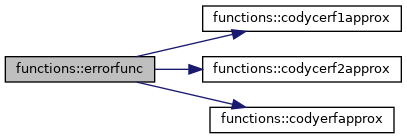
◆ errorfunc()

elemental real function, public functions::errorfunc ( real, intent(in) x )

returns the error function of argument x calculation of error fuction and complementary errorfunction are based on M. Abramowitz and I. A. Stegun: Handbook of Mathematical Functions, Applied Mathematics Series. National Bureau of Standards, Vol. 55, 1964 online resource: http://people.math.sfu.ca/~cbm/aands/ and "Rational Chebyshev approximations for the error function" by W. J. Cody, Math. Comp., 1969, PP. 631-638. Coefficients for the Polynoms are taken from the library routine http://www.netlib.org/specfun/erf written by W. J. Cody

Definition at line 918 of file functions.f90.

Here is the call graph for this function:

Here is the caller graph for this function:

◆ gamma()

elemental real function, public functions::gamma ( real, intent(in) x )

Compute the Gamma function for arguments != 0,-1,-2,..

x Gamma(x)

1/3 2.678938534708 0.5 1.772453850906 -0.5 -3.544907701811 -1.5 2.363271801207 5.0 24.000000000000

Definition at line 1132 of file functions.f90.

Here is the caller graph for this function:

◆ heaviside()

elemental real function, public functions::heaviside	(	real, intent(in)	x,
		real, intent(in)	a
	)

step function

Definition at line 131 of file functions.f90.

Here is the caller graph for this function:

◆ incompleteellipticintegral_e()

elemental real function, public functions::incompleteellipticintegral_e	(	real, intent(in)	phi,
		real, intent(in)	ak
	)

Legendre elliptic integral of the second kind E(phi,k), evaluated using Carlson's function R_D and R_F. The argument ranges are 0 <= phi <= pi/2, 0 <= k*sin(phi) <= 1 similar to Numerical recipes 2nd edition.

Definition at line 425 of file functions.f90.

Here is the call graph for this function:

◆ incompleteellipticintegral_f()

elemental real function, public functions::incompleteellipticintegral_f	(	real, intent(in)	phi,
		real, intent(in)	ak
	)

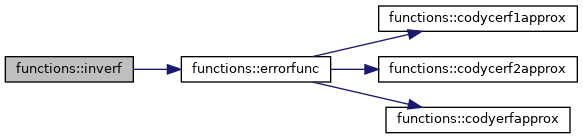
Definition at line 407 of file functions.f90.

Here is the call graph for this function:

◆ inverf()

elemental real function, public functions::inverf ( real, intent(in) x )

Inverse of the error function Argument of this function has to be in ]-1,1[, returns huge(1.0) for values x with abs(x)>=1 without an error !!!! uses and idea of P.J. Acklam http://home.online.no/~pjacklam/notes/invnorm/ to calculate the inverse using the Halley root finding algorithm Halley is preferable to Newton- Raphson as the second derivative can be computed easily f''(y) = -2y*f'(y) for f(y)=erf(y)

Definition at line 1090 of file functions.f90.

Here is the call graph for this function:

◆ legendrefunction_qminhalf()

elemental real function, public functions::legendrefunction_qminhalf ( real, intent(in) x )

Computation of the order 0 and -1/2 degree Legendre function of the second kind Q_{-1/2} using the AGM method (arithmetic-geometric-mean)

returns NaN on error, i.e. for x <= 1

Definition at line 538 of file functions.f90.

◆ legendrepolynomial_all()

elemental real function functions::legendrepolynomial_all	(	integer, intent(in)	l,
		real, intent(in)	x
	)

private

Definition at line 510 of file functions.f90.

Here is the call graph for this function:

◆ legendrepolynomial_one()

elemental real function functions::legendrepolynomial_one	(	integer, intent(in)	l,
		real, intent(in)	x,
		real, intent(in)	Plminus1,
		real, intent(in)	Plminus2
	)

private

Definition at line 478 of file functions.f90.

Here is the caller graph for this function:

◆ legendrepolynomials()

pure subroutine, public functions::legendrepolynomials	(	integer, intent(in)	l,
		real, intent(in)	x,
		real, dimension(0:l), intent(out)	P
	)

Definition at line 441 of file functions.f90.

◆ lngamma()

elemental real function, public functions::lngamma ( double precision, intent(in) x )

computes the logarithm of the gammafunction with Lanczos approximation found in Numerical Recipes for C++ p. 257 (different implementation) coefficiants from Paul Godfrey for g=607/128 and N=15 http://my.fit.edu/~gabdo/gamma.txt Gamma(x+1)=x!

Definition at line 1196 of file functions.f90.

Here is the caller graph for this function:

◆ normalrand()

elemental subroutine, public functions::normalrand	(	real, intent(in)	u1,
		real, intent(in)	u2,
		real, intent(out)	x,
		real, intent(out)	y
	)

Box-Muller alg. for gaussian distributed random variables input are uniform distributed random variables [0,1)

Definition at line 151 of file functions.f90.

◆ power_series_ei()

elemental real function functions::power_series_ei ( real, intent(in) x )

private

Definition at line 821 of file functions.f90.

Here is the caller graph for this function:

◆ rd()

elemental real function functions::rd	(	real, intent(in)	x,
		real, intent(in)	y,
		real, intent(in)	z
	)

private

Computes Carlson's elliptic integral of the second kind R_D(x,y,z), y,y > 0. One can be zero. z > 0. TINY must be at least twice -2/3 power of the machine underflow limit, BIG at most 0.1 x ERRTOL times the -2/3 power of the machine overflow limit. similar to Numerical recipes 2nd edition.

Definition at line 346 of file functions.f90.

Here is the caller graph for this function:

◆ rf()

elemental real function functions::rf	(	real, intent(in)	x,
		real, intent(in)	y,
		real, intent(in)	z
	)

private

Computes Carlson's elliptic integral of the first kind R_F(x,y,z), y,y,z > 0. One can be zero. TINY must be at least 5x the machine underflow limit, BIG at most one fifth of the machine overflow limit. similar to Numerical recipes 2nd edition.

Definition at line 291 of file functions.f90.

Here is the caller graph for this function:

Variable Documentation

◆ eps_agm

real, parameter functions::eps_agm = EPSILON(EPS_AGM)

private

Definition at line 54 of file functions.f90.

◆ iii

integer functions::iii

private

Definition at line 57 of file functions.f90.

◆ max_agm_iterations

integer, parameter functions::max_agm_iterations = 20

private

Definition at line 55 of file functions.f90.

◆ max_pl_coeff

integer, parameter functions::max_pl_coeff = 20

private

Definition at line 58 of file functions.f90.

◆ pi

real, parameter functions::pi = 3.14159265358979323846

private

Definition at line 52 of file functions.f90.

◆ pl_coeff

real, dimension(max_pl_coeff), parameter functions::pl_coeff = (/ (iii/(iii+1.0), iii=1,MAX_PL_COEFF) /)

private

Definition at line 59 of file functions.f90.

◆ sqrt_two

real, parameter functions::sqrt_two = 1.41421356237309504880

private

Definition at line 53 of file functions.f90.

Functions/Subroutines

Variables

Detailed Description

Function/Subroutine Documentation

◆ acosh()

◆ argument_addition_series_ei()

◆ asinh()

◆ atanh()

◆ barrier()

◆ bessel_i0()

◆ bessel_i1()

◆ bessel_k0()

◆ bessel_k0e()

◆ bessel_k1()

◆ codycerf1approx()

◆ codycerf2approx()

◆ codyerfapprox()

◆ comperrorfunc()

◆ continued_fraction_ei()

◆ ei()

◆ ellipticintegral_e()

◆ ellipticintegral_k()

◆ ellipticintegrals()

◆ errorfunc()

◆ gamma()

x Gamma(x)

◆ heaviside()

◆ incompleteellipticintegral_e()

◆ incompleteellipticintegral_f()

◆ inverf()

◆ legendrefunction_qminhalf()

◆ legendrepolynomial_all()

◆ legendrepolynomial_one()

◆ legendrepolynomials()

◆ lngamma()

◆ normalrand()

◆ power_series_ei()

◆ rd()

◆ rf()

Variable Documentation

◆ eps_agm

◆ iii

◆ max_agm_iterations

◆ max_pl_coeff

◆ pi

◆ pl_coeff

◆ sqrt_two