How to Interpret the Measurement Results

Joachim Köppen Kiel 2020

If we want to interpret our measurements in a quantitative and meaningful way - and to get thrustworthy values for the antenna temperature and the radio flux of a source - we need to know the characteristics of the receiving system. This information is obtained by Flux Calibrations.

Suppose we have measured from a source at elevation ε the power p(source), as well as the sky background next to the source, but at the same elevation, which gave the power p(sky).

If there were no noise from the Earth atmosphere or the CMB, and if we knew the system temperature, the analysis would be very easy: Two measurements of source and sky give the two equations

which are solved for the two unknowns

But we must know the system temperature, or take the value from an earlier measurement and assume that it was constant... Unfortunately, on 11 GHz the noise background from the sky and from the receiver (temperature!) may change quite rapidly. Thus, it is strongly advisable to make a flux calibration before and after the proper observation. Here is an example from 2007 of two solar drift scans sandwiched between calibration measurements:

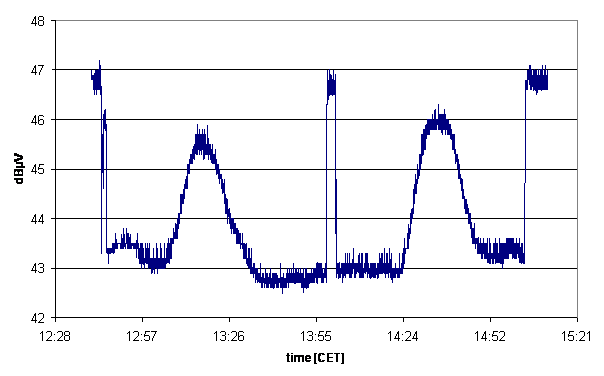
In a simple approach we make a third measurement: of the flux calibrator. This adds another equation

and the system of three equations are solved for the three unknowns

But reality is not that simple: There is not only the contribution of the CMB, but - more importantly - the Earth atmosphere has a thermal emission which is present in all measurements in the sky. The latter might more appropriately called the sky 'foreground' as it adds on the line-of-sight between the source and the telescope. Thus the correct analysis of data requires complete flux calibrations to get the full information on the system and the sky conditions ...

If we know system temperature T_sys, scaling factor a, and zenith temperature T_zen, we can compute the antenna temperature of the source:

It is a good idea to check whether the measured power of the sky background matches indeed the predicted sky noise at this elevation:

If this does not agree, evidently the sky conditions and/or the system properties have changed - which is quite possible on 11 GHz! We might then again resort to the three equations from the three measurements of source, sky, and flux calibrator:

from which only three unknowns can be determined. Since we want to know T_source, we may freely choose two other parameters as unknown: if we took T_sys and a, we obviously assume that the weather has not changed.
Choosing T_sys and T_zen might be a bit problematic, because the determination of the zenith temperature would hinge on only a single measurement at one elevation ε. Of course, a full sky noise measurement at several elevations would take time ...
An alternative to such a lengthy full treatment would be to measure the sky background at only a few elevations ...
Or we could make some reasonable assumptions for e.g. the zenith temperature, ... so based on the available data and information we have to make a decision what to assume, what to approximate, what to neglect! We must be aware that this will be a compromise, which puts limits on the accuracy of the results. Note that this also depends on the strength of the source signal: the weaker the source, the more critical is the treatment of the sky background...

Whatever is your decision you'll get the source's antenna temperature. This value is a measure of the power received by the antenna:

The effective area of the antenna can be computed from the effective diameter - which may be taken as the diameter of a uniformly illuminated dish which gives the same HPBW of the main antenna lobe:

Thus the radio flux from the source can be computed:

with the factor of two to account for the fact that the unpolarized radio noise is received by the antenna in only one polarization state.

| Top of the Page | Back to the MainPage | to my HomePage |

last update: Oct 2020 J.Köppen