Basic Data Reduction

Joachim Köppen Strasbourg 2007

Please consult also: Solar Observations and Lunar Observations which contain hints for data reduction under more difficult conditions.

Since in radio astronomy we observe signal close to the noise, we need to reduce carefully the raw data, before we can really use and interpret it. What needs to be done is this

• our data is in units of dBµV, a logarithmic measure of the power, relative to a signal of 1µV at the receiver's input terminal: dBµV

  

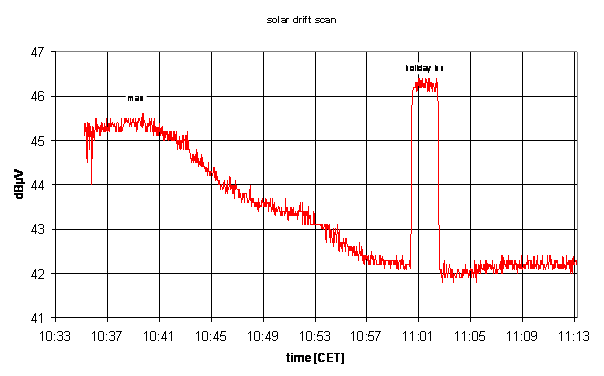
• we first need to convert into a linear measure of power, by applying to all data
  datum = 10**( dBµV / 10)
• next, we determine the background power level, by averaging over a sufficiently long stretch of data obtained in the empty sky:
  background
  of course, this is already in linear units!
• in the same way, we determine the level of the calibration, from the pointings on the Holiday Inn:
  calibration
• now we can reduce all data, by subtracting the background and calibrate the data to the power of the calibration: power = (raw_datum - background)/(calibration - background)

  

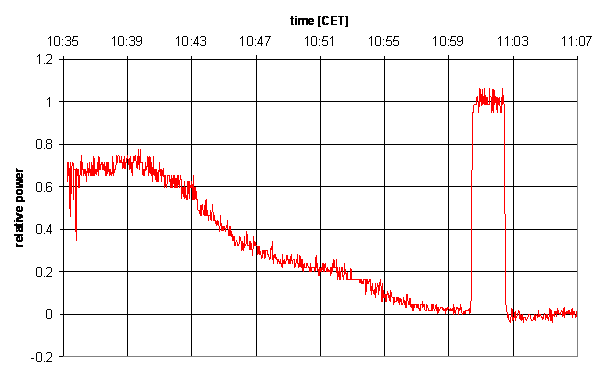
• often the fluctuations in the curve are still rather large. So one could apply a smoothing of the data by averaging over a number of data points. This was done here:

  

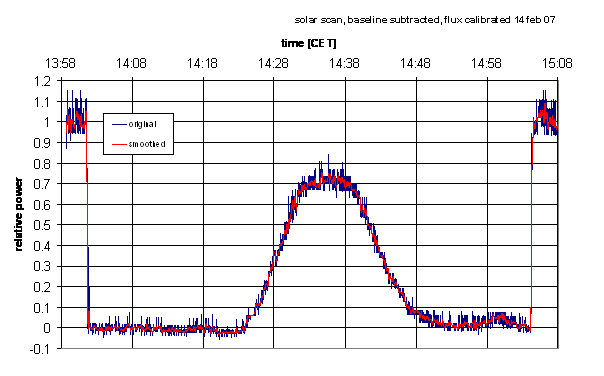
• if we multiply with the temperature of the calibrator, we get the Antenna temperatures T_ant = power * 300 K
• if the background and/or the calibrator levels change with time, one could apply a linear interpolation of these levels between the initial and final values ... but sometimes these variations do not seem to follow such a simple time dependence. Thus, the only thing one can do is to take constant values for background and/or calibration, and simply accept that the antenna temperature can have excursions into negative values ... Analysis may be tricky, but that's reality of doing observations!

If you want to interpret data of the Moon or the Sun, you also need two more data which you'll get from the prediction applet:

• If you want to convert the times into angular degrees, for instance when you want to get from a full drift scan the antenna pattern in true degrees, you need to know the speed with which the sun crosses the sky. This is close to 15 degrees per hour (360 degrees per day! or 1° in 4 minutes) ... but only when the Sun is located on the celestial equator, i.e. on 21 march and 21 september. For any other times, the angular speed is somewhat less. It depends on the actual Declination δ of the Sun or Moon (be sure you don't confuse with the Elevation angle!). We apply this formula: angular speed = 15°/hour * cos(Declination) Since in winter and in summer the Sun will be at declinations as much as -27° and +27°, respectively, the angular speed can be as low as 13.3°/hour!
• the angular diameter. This is necessary for conversion of the antenna temperature into true surface temperature: T_surface = T_ant * (antenna HPBW/angular diameter)² This factor arises because the Sun has an angular size less than the HPBW, so its radiation does not fill the antenna beam completely, but the calibrator signal does it. Hence to give the same received power, i.e. same antenna temperature, the Sun must be correspondingly hotter.

| Top of the Page | Back to the MainPage | to my HomePage |

last update: May 2013 J.Köppen