Noise of the Earth Atmosphere (10 GHz)
Joachim Köppen, Strasbourg, 2011/12
Objective: While the observation of a celestial source is affected by
the noise background from the receiver as well as from the earth atmosphere,
the measurement of the calibrator is only subjected to the receiver
noise. Since the sky noise depends on elevation angle in a known way, but
the receiver noise is constant, measurement of the noise of the 'empty' sky
at several elevation angles allows to separate the two contributions, and
a more correct value for the antenna temperature is obtained.
Observations
Follow the procedures to
switch-on the ESA-Dresden telescope
- Goto Calibrator and Start Observe & Record; measure
here for about 5 min
- At the same azimuth, move the telescope manually to at least four
elevations: 10°, (15°), 20°, (25°), 30°, (40°), 60°. At each
position measure for about 5 min. The signal level should decrease
slightly with elevation.
- Finish by Goto Calibrator, stay another 5min, and
then Stop & Finish the observations
Interpretation (more details):
- Import the text file with the data into Excel
- Convert all the dBµV values into linear units (P = 10^(dB/10))
- For each elevation, take the average value of all the measurements
- plot these data against 1/sin(EL) - the value of airmass in a
planar atmosphere
- Fit a straight line to the data:
- Its intersection with the y-axis gives the noise level of
the receiver (plus the cosmic microwave background) = P0
- The slope gives the atmospheric contribution to the
background noise = slope
- Application: With these parameters, the true antenna temperature
of a celestial source (sun, moon) can be determined:
Tant = 290K * (Psource - Psky(EL))/(Pcal P0)
where the sky background Psky(EL) at the source's elevation
EL is either measured or computed from the fit formula
Psky(EL) = P0 + slope/sin(EL)
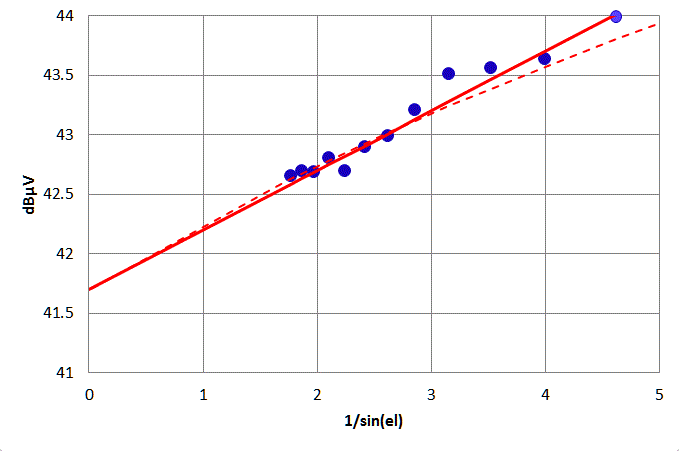 In the plot above, I simply did the linear fit on the dBµV values
instead of converting them (more accurately) to linear powers ...
In the plot above, I simply did the linear fit on the dBµV values
instead of converting them (more accurately) to linear powers ...
- Using the flux calibrator measurements (Pcal), and neglecting
the contribution from the cosmic microwave background, we can
express the measurements in Kelvin above the constant background:
T = 290K * (P - P0)/(Pcal P0)
- [if we had a second calibration source, of a much lower
temperature, we could also separate the receiver noise from
the CMB radiation
]
| back to Main page
| ESA-Haystack Radio Telescope (1.4 GHz)
| ESA-Dresden Ratio Telescope (10GHz)
| to my HomePage
|
last update: Sept. 2011 J.Köppen
