System temperature of ESA-Haystack

Determine the System Temperature

Joachim Köppen Strasbourg 2011

One very important parameter of a radio telescope is the "System temperature". This quantity measures the overall sensitivity of the receiving system, that is the receiver and the antenna. Because the noise background in a radio telescope system is almost always a dominant factor in the measurements, one always observes not only the particular source of interest, but also makes a measurement of an empty patch of the sky nearby. Thus we measure the power P_on at the position of the source and at an offset position P_off. The ratio is usually called Y and can be expressed in terms of antenna temperatures

Y = P_on/P_off = (T_source + T_system) / (T_sky + T_system) We keep in mind that the antenna temperature is simply a convenient way of expressing the power measured in each case, and that the formula simply distinguishes between the power coming from the source, the sky, and any noise from the receiving system itself. The system noise is mainly the noise produced by the receiver itself, in particular the first active device in the preamplifier, any losses between the antenna feed and the preamplifier, any contribution of thermal emission from the ground and the surroundings, which may play a role, as the focus assembly may pickup radiation from behind the parabolic dish, either by the receiver seeing a bit outside the reflector (antenna "spill-over") or seeing through the wire mesh of the reflector ("feed-thru"). Finally, in principle there is emission from the sky and clouds. All these noise sources would be characterized by their contribution, but here, for simplicity, we lump all of them together in one quantity.

At 21 cm and for our small telescope, we may neglect the emission from the sky: T_sky = 0. Hence we can express the system temperature as

T_system = T_source / (Y-1)

However... it isn't all that simple: the thermal emission from the Earth atmosphere plays quite an important role in the background noise, particularily at lower elevations. See Flux Calibration and System Temperature and How to Interpret Measurements for a more comprehensive treatment!

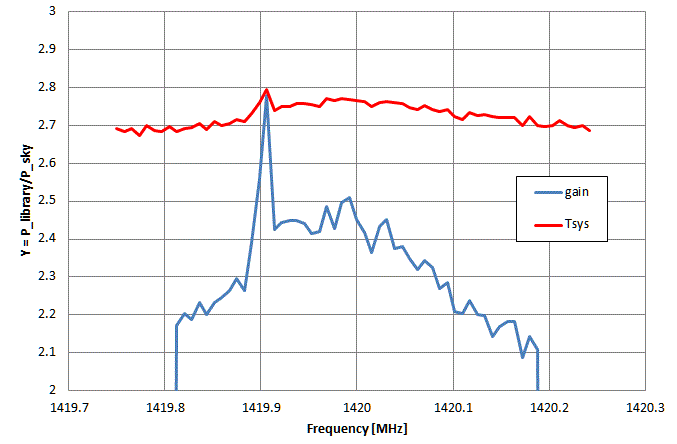
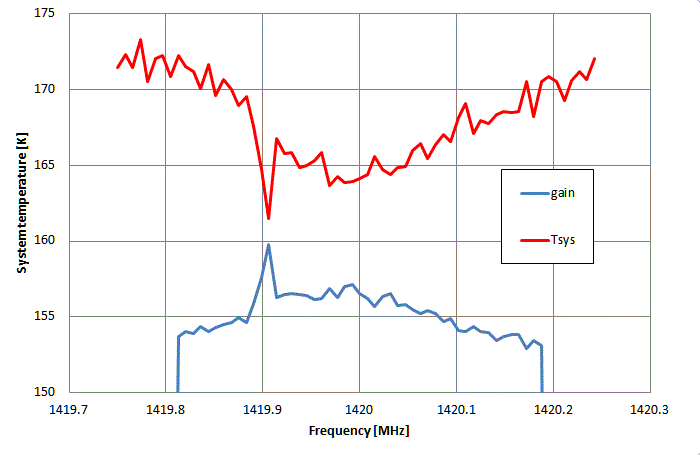
The simplest, easiest, but also the most fundamental way is to use the wall of our library as a calibration source: it fills the entire antenna beam and we may well assume its physical temperature to be close to 290 K - if we required a higher accuracy, we could use a thermometer to measure it. We measure with a wide frequency span the spectrum of the library wall - our Stow sposition - and then at some sky position, such as AZ=1° EL=60°. From the recorded spectra we compute Y and then the system temperature and plot them as a function of frequency:

The very narrow feature at 1419.9 MHz is a local interference carrier present in the Stow spectrum, at 1420.4 MHz there is some galactic emission picked up at the Sky position. It can be seen that the maximum response of the system (i.e. filter and preamplifier) peaks at about 1420.4 MHz. However, the lowest system temperature occurs at a different frequency 1419.3 MHz. Thus power matching and noise matching do not necessarily coincide.

On the first day of our operations, we did a complete solar observation and determined the system temperature:

since our counts (cts) are strictly proportional to the power, we can determine Y = Stow/Sky = 3599/1318 = 2.73 (or 4.4 dB) from averaging over the spectrum
this gives a system temperature of 168K (which is the value we should expect from the manufacturer's information)
for the Sun we get Y = Sun/Sky = 5180/1318 = 3.933 (or 5.9 dB)
this gives an antenna temperature of the Sun: 490 K

A closer look at the average spectra taken at Stow and Sky positions gives

The best system temperature of 164 K is found just below 1420 MHz, and it also coincides with the peak response.

We may go one step further:

We know the power received from the Sun in absolute terms P_sun = 2 k T_sun with Boltzmann's constant k = 1.38 E-23 Ws/K. The factor of 2 takes into account that the solar emission is unpolarized, but the antenna measures only one polarization state. Using more convenient units for radio astronomy (1 Jansky = 1 Jy = 1E-26 Ws/m²) we get P_sun = 2760 T_sun = 1352400 Jy m² = 135 SFU m² (solar flux units)
Our antenna of diameter 2.3m has a geometrical cross section of 4.15 m², hence the measured solar flux would be 135/4.15 = 32.5 SFU
However, from NOAA we know the solar flux measured by professional stations on that day on 1415 MHz as 54 SFU.
Consequently, we can compute the efficiency of our telescope as 32.5/54 = 0.6. This means that the effective collecting surface of the telescope is only about 2.5m, which corresponds to an effective diametre of 1.8m. These figures are well in agreement of what one can expect. Perhaps some optimization of the antenna could improve these numbers somewhat.

This first measurement was before the growing interference became so severe, that we had to install narrow band filters in front of the preamplifier. The inevitable insertion loss of the filters degrades the telescope's performance. The best system temperature reached so far is about 300 K. But we successfully surveyed the emission of the Milky Way even with system temperatures of 1000 K!

| Top of the Page | Back to the MainPage | to my HomePage |

last update: Oct 2020 J.Köppen