Solar Flux, HPBW and System Temperature of ESA-Dresden (10 GHz)

Joachim Köppen, Strasbourg, 2011/12

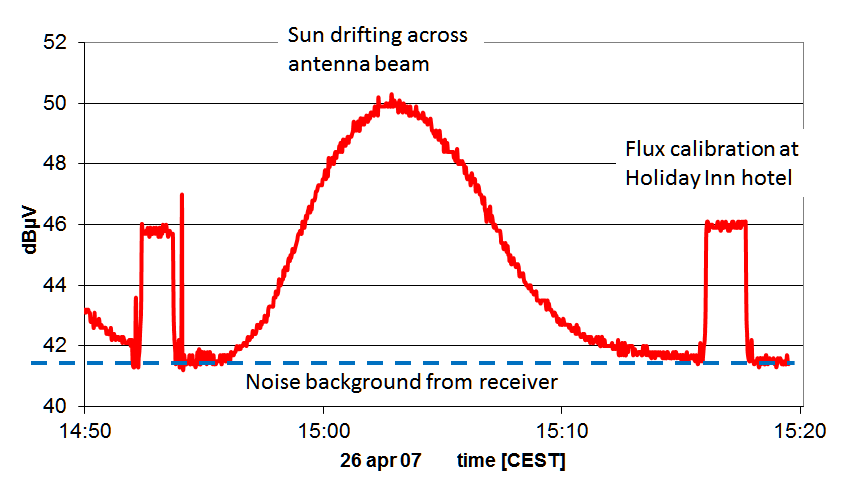
From full drift scans of the sun (see for How to observe or archive data) one can also extract information on the telescope:

• Import the text file with the data into Excel
• Convert all measurements from dBµV values into linear powers (P = 10^(dBµV/10))
• To remove or reduce the fluctuations in the measured values, apply a 'boxcar' running mean smoothing: for each datum compute the average of about 20 points before and after this instant. You could also use a Gaussian function ...
• Determine the sky background value: Psky
• Determine the flux calibrator value: Pcal
• Convert all measured powers into antenna temperatures
  Tant = 290 K * (P – Psky) / (Pcal – Psky)
• Plot the antenna temperature as function of time (scatter plot)
• Make sure that the measurements of the sky average about zero temperature, while the calibrator measurements are around 290 K. If not, adjust Psky and Pcal …
• Determine the times at which the bell-shaped curve of solar measurements reaches the half of the maximum value.
• Convert this time span into the angle that the sun had moved. This is 15°/min*cosδ with the present declination δ of the sun (e.g. from here)
• This angle is the Half Power Beam Width of the antenna.
• One may also compare the measured curve with a Gaussian function, and get its width from a best fit.
• The system temperature is computed from
  Tsys = 290K / (1-Pcal/Psky)
• In this derivation, we have assumed that the sky background measured at the elevation of the sun is the noise background of the system. However, this is not entirely correct: The sky noise has two components: a contribution from the atmosphere which depends like 1/sinEL on elevation, and a constant one from the receiver itself as well as from the cosmic microwave background. To separate them, one must observe the sky at several elevations. In which way does the system temperature change?

• From the maximum of the solar drift scan, we can compute the antenna temperature of the sun from
  Tant_sun = 290 K * (Pmax – Psky) / (Pcal – Psky)
• The antenna beam’s solid angle is Ω = π/4 * (HPBW*π/180°)²
• This gives its effective area: Aeff = λ²/Ω
• The flux F = 2 k Tant_sun/Aeff can be compared with the data for that day and frequency published by NOAA (note that 1 SolarFluxUnit = 10000 Jy)
• However, our flux might not be equal to the NOAA flux. It is very likely that our value for the effective area is not correct! Indeed, we can use the flux measurements to compute the effective area of our telescope ... and then compute its efficiency = Aeff/Ageometry. Values between 0.5 and 0.9 would be realistic.

| back to Main page | ESA-Haystack Radio Telescope (1.4 GHz) | ESA-Dresden Ratio Telescope (10GHz) | to my HomePage |

last update: Sept. 2011 J.Köppen