computes momentum and energy sources due to shear stresses More...
Data Types | |
| type | sources_viscosity |
Functions/Subroutines | |
| subroutine | initsources (this, Mesh, Physics, Fluxes, config, IO) |
| subroutine | setoutput (this, Mesh, config, IO) |
| subroutine | infosources (this) |
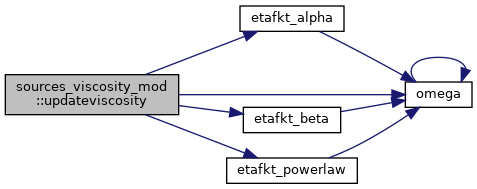
| subroutine | updateviscosity (this, Mesh, Physics, Fluxes, time, pvar, cvar) |
| updates dynamic and bulk viscosity More... | |
| subroutine | externalsources (this, Mesh, Physics, Fluxes, Sources, time, dt, pvar, cvar, sterm) |
| subroutine | calctimestep (this, Mesh, Physics, Fluxes, pvar, cvar, time, dt, dtcause) |
| compute time step limit for advection-diffusion problems More... | |
| subroutine | finalize (this) |
| destructor More... | |
Variables | |
| character(len=32), parameter | source_name = "viscosity of Newtonian fluid" |
| integer, parameter, public | molecular = 1 |
| integer, parameter, public | alpha = 2 |
| integer, parameter, public | beta = 3 |
| integer, parameter, public | powerlaw = 4 |
| integer, parameter, public | alpha_alt = 5 |
| character(len=32), dimension(5), parameter, public | viscosity_name = (/ "constant viscosity ", "turbulent Shakura-Sunyaev ", "turbulent Duschl ", "power law viscosity ", "alternative Shakura-Sunyaev "/) |
Detailed Description
computes momentum and energy sources due to shear stresses
The momentum sources are given by the divergence of the stress tensor \( \nabla\cdot\mathbf{T} \) whereas the energy source term, i.e. heating due to dissipation, is given by the divergence of the stress tensor projected on the velocity field \( \nabla\cdot\left(\mathbf{T}\cdot\mathbf{v}\right) \) .
The components of the stress tensor
\[ \mathbf{T} = \eta\left(\nabla\mathbf{v} + \nabla\mathbf{v}^\mathsf{T}\right) + \mu_\mathrm{b} \nabla\cdot\mathbf{v} \]
are computed in the physics modules, see e.g. physics_eulerisotherm::calcstresses for any given curvilinear orthonormal geometry.
For a description of the currently supported (effective turbulent) viscosity models see updateviscosity
Function/Subroutine Documentation
◆ calctimestep()
| subroutine sources_viscosity_mod::calctimestep | ( | class(sources_viscosity), intent(inout) | this, |
| class(mesh_base), intent(in) | Mesh, | ||
| class(physics_base), intent(inout) | Physics, | ||
| class(fluxes_base), intent(in) | Fluxes, | ||
| class(marray_compound), intent(inout) | pvar, | ||
| class(marray_compound), intent(inout) | cvar, | ||
| real, intent(in) | time, | ||
| real, intent(inout) | dt, | ||
| integer, intent(out) | dtcause | ||
| ) |
compute time step limit for advection-diffusion problems
The limiting time step is computed according to the analysis of [22] (see also [37] ) for explicit Euler time-stepping with spatial upwinding for the advective transport step (see eq. (99) in [22] ).
Definition at line 511 of file sources_viscosity.f90.
◆ externalsources()
|
private |
Definition at line 481 of file sources_viscosity.f90.
◆ finalize()
|
private |
destructor
Definition at line 584 of file sources_viscosity.f90.
◆ infosources()
|
private |
Definition at line 296 of file sources_viscosity.f90.
◆ initsources()
|
private |
- Todo:
- check if this is really sufficient
Definition at line 118 of file sources_viscosity.f90.
◆ setoutput()
| subroutine sources_viscosity_mod::setoutput | ( | class(sources_viscosity), intent(in) | this, |
| class(mesh_base), intent(in) | Mesh, | ||
| type(dict_typ), pointer | config, | ||
| type(dict_typ), pointer | IO | ||
| ) |
Definition at line 260 of file sources_viscosity.f90.
◆ updateviscosity()
| subroutine sources_viscosity_mod::updateviscosity | ( | class(sources_viscosity), intent(inout) | this, |
| class(mesh_base), intent(in) | Mesh, | ||
| class(physics_base), intent(inout) | Physics, | ||
| class(fluxes_base), intent(in) | Fluxes, | ||
| real, intent(in) | time, | ||
| class(marray_compound), intent(inout) | pvar, | ||
| class(marray_compound), intent(inout) | cvar | ||
| ) |
updates dynamic and bulk viscosity
Currently 5 different viscosity prescriptions are supported
- molecular: constant dynamic and bulk viscosity coefficients (no temperature dependence implemented yet)
- alpha: Shakura-Sunyaev \( \alpha \)-viscosity [46]
The kinematic effective turbulent viscosity is set according to\[ \nu = \alpha \frac{c_s^2}{\Omega} \]
with \( \alpha < 1 \) . It can be derived from the ansatz\[ T_{r\varphi} = \nu \Sigma r \frac{d\Omega}{d r} = -\tilde{\alpha} \Pi \]
using \( \Pi = \gamma c_s^2 \Sigma \) and\[ A = \left(-\frac{d\ln\Omega}{d\ln r}\right)^{-1} \approx \frac{2}{3}. \]
where the approximation holds for Keplerian disks (see [26] , Section 3.2.1). The two non-dimensional parameters are then related according to \( \alpha = \tilde{\alpha} \gamma A \). - alpha_alt: alternative Shakura-Sunyaev \( \alpha \)-viscosity [46]
This is an alternative derived from the prescription above using the relation \( c_s = h \Omega \) to replace one \( c_s \) in the viscosity formula:\[ \nu = \alpha c_s h \]
Attention! This works only for geometrically thin Keplerian disks and requires computation of the pressure scale height \( h \) (see sources_gravity_mod::calcdiskheight ) - beta: Duschl-Strittmatter-Biermann \( \beta \)-viscosity [11]
The kinematic effective turbulent viscosity is set according to\[ \nu = \beta r v_\varphi = \beta r^2 \Omega \]
with local angular velocity \( \Omega \) and dimensionless parameter \( \beta \approx \mathfrak{Re}_\mathrm{crit}^{-1} \ll 1 \) where the critical Reynolds number is of the order of \( 10^3 \) . - powerlaw: kinematic viscosity scales with power law depending on specific angular momentum:
\[ \nu = \nu_0 / \ell_0^q \ell^q = \beta \ell^q \]
In cases 2. – 5. bulk viscosity \( \mu_\mathrm{b} \) is set using the Stokes' hypothesis, namely that the volume viscosity is zero, i.e.
\[ \zeta = 0 \Leftrightarrow \mu_b = -\frac{2}{3}\eta \]
.
Definition at line 356 of file sources_viscosity.f90.
Variable Documentation
◆ alpha
| integer, parameter, public sources_viscosity_mod::alpha = 2 |
Definition at line 76 of file sources_viscosity.f90.
◆ alpha_alt
| integer, parameter, public sources_viscosity_mod::alpha_alt = 5 |
Definition at line 79 of file sources_viscosity.f90.
◆ beta
| integer, parameter, public sources_viscosity_mod::beta = 3 |
Definition at line 77 of file sources_viscosity.f90.
◆ molecular
| integer, parameter, public sources_viscosity_mod::molecular = 1 |
Definition at line 75 of file sources_viscosity.f90.
◆ powerlaw
| integer, parameter, public sources_viscosity_mod::powerlaw = 4 |
Definition at line 78 of file sources_viscosity.f90.
◆ source_name
|
private |
Definition at line 73 of file sources_viscosity.f90.
◆ viscosity_name
| character(len=32), dimension(5), parameter, public sources_viscosity_mod::viscosity_name = (/ "constant viscosity ", "turbulent Shakura-Sunyaev ", "turbulent Duschl ", "power law viscosity ", "alternative Shakura-Sunyaev "/) |
Definition at line 80 of file sources_viscosity.f90.
 1.9.4
1.9.4